
【题目】(1)在下面的括号内,填上推理的依据.
①如图1,![]() ,求证
,求证![]()
证明:![]()
![]() ,
,
![]()
![]() (_____________)
(_____________)
![]() (_____________)
(_____________)
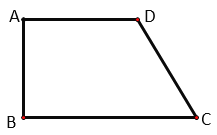
②如图2,![]() ,求证
,求证![]()
证明:![]() ,
,
![]() (_____________)
(_____________)
![]()
![]() (_____________)
(_____________)
![]() (_____________)
(_____________)
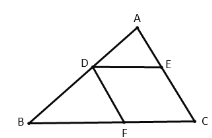
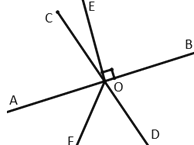
(2)如图,直线![]() 相交于点
相交于点![]() 平分
平分![]() 求①
求①![]() 的度数;②
的度数;②![]() 的度数.
的度数.
【答案】(1)①同旁内角互补,两直线平行; 两直线平行,同旁内角互补;
②两直线平行,同位角相等;两直线平行,内错角相等;等量替换;
(2)①![]() ;
;
②![]() .
.
【解析】
(1) ①先分析∠A,∠B的位置关系,即可写出直线平行的判定方法;再根据∠C,∠D的位置关系,即可写出平行的性质;
②分析![]() 和
和![]() 以及
以及![]() 的位置关系即可得到答案;
的位置关系即可得到答案;
(2)①要求![]() 的度数,根据角平分线的性质把
的度数,根据角平分线的性质把![]() 的度数计算出来,即可得到
的度数计算出来,即可得到![]() 的度数.
的度数.
②根据![]() 和
和![]() 把∠AOF的度数求解出来,即可得到
把∠AOF的度数求解出来,即可得到![]() 的度数;
的度数;
(1) 根据题意,得到括号里面分别为:
①同旁内角互补,两直线平行;
两直线平行,同旁内角互补;
②两直线平行,同位角相等;
两直线平行,内错角相等;
等量替换;
(2) ①∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
②由题意可知,
![]() ,
,
∵OF平分![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
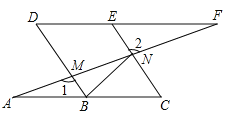
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图像的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+5,其中y1的图像经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当
2≤x≤3时,y2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小赵为班级购买笔记本作为晚会上的奖品回来时向生活委员交账说:“一共买了![]() 本,有两种规格,单价分别为
本,有两种规格,单价分别为![]() 元和
元和![]() 元去时我领了
元去时我领了![]() 元,现在找回
元,现在找回![]() 元”生活委员算了一下,认为小赵搞错了.
元”生活委员算了一下,认为小赵搞错了.
(1)请你用方程的知识说明小赵为什么搞错了.
(2)小赵一想,发觉的确不对,因为他把自己口袋里的零用钱一起 当做找回的钱给了生活委员.如果设购买单价为![]() 元的笔记本
元的笔记本![]() 本,试用含
本,试用含![]() 的代数式表示小赵零用钱的数目: 元
的代数式表示小赵零用钱的数目: 元
(3)如果小赵的零用钱数目是整数,且少于![]() 元,试求出小赵零用钱的数目.
元,试求出小赵零用钱的数目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一次函数y=﹣![]() x+2的图象分别与x轴、y轴交于点A、B.
x+2的图象分别与x轴、y轴交于点A、B.
(1)请直接写出A,B两点坐标:A 、B
(2)在直角坐标系中画出函数图象;
(3)若平面内有一点C(5,3),请连接AC、BC,则△ABC是 三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张看上去无差别的卡片,上面分别写着0,π, ![]() ,
, ![]() ,1.333,背面朝上放在不透明的桌子上,若随机抽取1张,则取出的卡片上的数是无理数的概率是( )
,1.333,背面朝上放在不透明的桌子上,若随机抽取1张,则取出的卡片上的数是无理数的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.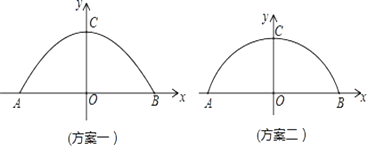
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com