
【题目】在平面直角坐标系中,![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
![]() 如图
如图![]() ,求
,求![]() 的面积.
的面积.
![]() 若点
若点![]() 的坐标为
的坐标为![]() ,
,
①请直接写出线段![]() 的长为________(用含
的长为________(用含![]() 的式子表示);
的式子表示);
②当![]() 时,求
时,求![]() 的值.
的值.
![]() 如图
如图![]() ,若
,若![]() 交
交![]() 轴于点
轴于点![]() ,直接写出点
,直接写出点![]() 的坐标为________.
的坐标为________.
【答案】(1)8,(2)①|m-2|②![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)过点C作CD⊥x轴,垂足为D,过点B作BE⊥CD,交DC延长线于E,过点A作AF⊥BE,交EB延长线于F,由题意得出∴D(-3,0),E(-3,4),F(2,4).得出AD=5,CD=2,BE=3,CE=2,DE=4,BF=2,AF=4.S△ABC=S矩形ADEF-S△ACD-S△BCE-S△ABF,即可得出结果;
(2)①根据题意容易得出结果;
②由三角形面积关系得出方程,解方程即可;
(3)与待定系数法求出直线AC的解析式,即可得出点D的坐标.
(1)过点C作CD⊥x轴,垂足为D,过点B作BE⊥CD,交DC延长线于E,
过点A作AF⊥BE,交EB延长线于F.如图所示:
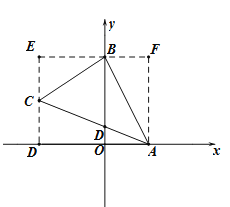
∵A(2,0),B(0,4),C(-3,2)
∴D(-3,0),E(-3,4),F(2,4).
∴AD=5,CD=2,BE=3,CE=2,DE=4,BF=2,AF=4.
∴S△ABC=S矩形ADEF-S△ACD-S△BCE-S△ABF
=ADDE ![]()
![]()
(2)①根据题意得:AP=|m-2|;
故答案为:|m-2|;
②∵![]()
∴![]()
∴![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ;
;
![]() 设直线
设直线![]() 的解析式为
的解析式为![]() ,
,
根据题意得:![]() ,
,
解得:![]() ,
,![]() ;
;
∴直线![]() 的解析式为
的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,;
,;
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次6元的包装费外,樱桃不超过1kg收费22元,超过1kg,则超出部分按每千克10元加收费用.设该公司从西安到南昌快递樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5kg樱桃,请你求出这次快寄的费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题的个数( )
(1)⊙O的半径为5,点P在直线l上,且OP=5,则直线l与⊙O相切
(2)在Rt△ABC中,∠C=90°,AC=5,BC=12,则△ABC的外接圆半径为6.5
(3)正多边形都是轴对称图形,也都是中心对称图形
(4)三角形的外心到三角形各边的距离相等.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
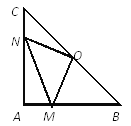
【题目】在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。
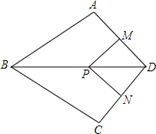
(1)求证:ADB=CDB;
(2)若ADC=90°,求证:四边形MPND是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知第一象限内的点A在反比例函数y= ![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y= ![]() 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA= ![]() ,则k的值为( )
,则k的值为( )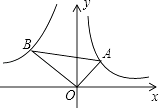
A.﹣3
B.﹣4
C.﹣ ![]()
D.﹣2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形纸片△ABC,AB=8,BC=6,AC=5,沿过点B的直线折叠这个三角形,折痕为BD(点D在线段AC上且不与A、C重合).若点C落在AB边下方的点E处,则△ADE的周长p的取值范围是( )

A. 7<p<10 B. 5<p<10 C. 5<p<7 D. 7<p<19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
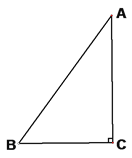
(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com