
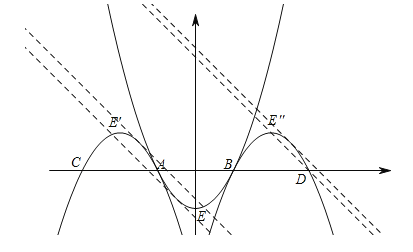
【题目】抛物线C1:y=x2﹣1(﹣1≤x≤1)与x轴交于A、B两点,抛物线C2与抛物线C1关于点A中心对称,抛物线C3与抛物线C1关于点B中心对称.若直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点,则b的取值或取值范围是_____.
【答案】b=-![]() 或-
或-![]() 或3
或3![]()
【解析】分析:根据对称性先求抛物线C2与抛物线C3的解析式,再分两种情况:
①在y轴右侧时,从直线y=﹣x+b与C3相切时到直线过点D时,这些b值符合条件,计算出来即可;
②在y轴的左侧,当y=﹣x+b与C1相切时和y=﹣x+b与C2相切时,都与C2有C1、C2、C3组成的图形恰好有2个公共点,分别计算出b的值.
详解:抛物线C1:y=x2﹣1(﹣1≤x≤1),顶点E(0,﹣1),当y=0时,x=±1,∴A(﹣1,0),B(1,0),当抛物线C2与抛物线C1关于点A中心对称,∴顶点E关于点A的对称点E′(﹣2,1),∴抛物线C2的解析式为:y=﹣(x+2)2+1=﹣x2﹣4x﹣3,当抛物线C3与抛物线C1关于点B中心对称,∴顶点E关于点B的对称点E′′(2,1),∴抛物线C3的解析式为:y=﹣(x﹣2)2+1=﹣x2+4x﹣3.分两种情况讨论:
①当y=﹣x+b过D(3,0)时,b=3,当y=﹣x+b与C3相切时,即与C3有一个公共点,则![]() ,﹣x2+4x﹣3=﹣x+b,x2﹣5x+b+3=0,△=25﹣4(b+3)=0,b=
,﹣x2+4x﹣3=﹣x+b,x2﹣5x+b+3=0,△=25﹣4(b+3)=0,b=![]() ,∴当3≤b<
,∴当3≤b<![]() 时,直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点;
时,直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点;
②当y=﹣x+b与C1相切时,即与C1有一个公共点,则![]() ,x2﹣1=﹣x+b,x2+x﹣1﹣b=0,△=1﹣4(﹣1﹣b)=0,b=﹣
,x2﹣1=﹣x+b,x2+x﹣1﹣b=0,△=1﹣4(﹣1﹣b)=0,b=﹣![]() ,当y=﹣x+b与C2相切时,即与C2有一个公共点,则
,当y=﹣x+b与C2相切时,即与C2有一个公共点,则![]() ,﹣x2﹣4x﹣3=﹣x+b,﹣x2﹣3x﹣3﹣b=0,△=9﹣4×(﹣1)×(﹣3﹣b)=0,b=﹣
,﹣x2﹣4x﹣3=﹣x+b,﹣x2﹣3x﹣3﹣b=0,△=9﹣4×(﹣1)×(﹣3﹣b)=0,b=﹣![]() ,∴当b=﹣
,∴当b=﹣![]() 或﹣
或﹣![]() 时,直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点.
时,直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点.
综上所述:当b=﹣![]() 或﹣
或﹣![]() 或3≤b<
或3≤b<![]() 时,直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点.
时,直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】已知![]() ∥
∥![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的两点,点
上的两点,点![]() 在
在![]() 、
、![]() 之间,连接
之间,连接![]() 、
、![]() .
.
(1)如图①,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,若点![]() 是
是![]() 下方一点,
下方一点,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,已知
,已知![]() ,求
,求![]() 的度数;
的度数;
(3)如图③,若点![]() 是
是![]() 上方一点,连接
上方一点,连接![]() 、
、![]() ,且
,且![]() 的延长线
的延长线![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,求
,求![]() 的度数.
的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:
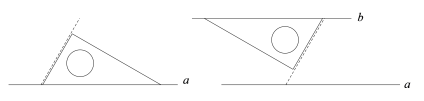
①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=![]() 的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列五个结论:
的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列五个结论:
①△CEF与△DEF的面积相等; ②△AOB∽△FOE;
③△DCE≌△CDF;④AC=BD; ⑤tan∠BAO=a
其中正确的结论是_____.(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
因式分解:![]() .
.
解:将“![]() ”看成整体,令
”看成整体,令![]() ,则原式
,则原式![]() .
.
再将“![]() ”还原,原式
”还原,原式![]() .
.
上述解题用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法.
(问题解决)
(1)因式分解:![]() ;
;
(2)因式分解:![]() ;
;
(3)证明:若![]() 为正整数,则代数式
为正整数,则代数式![]() 的值一定是某个整数的平方.
的值一定是某个整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,正整数的和1+3+5+…+(2n﹣1)=n2,若把所有正偶数从小到大排列,并按如下规律分组:(2),(4,6,8),(10,12,14,16,18),(20,22,24,26,28,30,32),…,现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到右数),如A8=(2,3),则A2018=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点B(0,2)的直线y=kx+b与x轴交于点C,与正比例函数y=ax的图象交于点A(﹣1,3)
(1)求直线AB的函数的表达式;
(2)直接写出不等式(kx+b)﹣ax<0的解集;
(3)求△AOC的面积;
(4)点P是直线AB上的一点,且知△OCP是等腰三角形,写出所有符合条件的点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com