
ЁОЬтФПЁПЧрЩйФъЪгСІЫЎЦНЯТНЕвбв§Ц№ШЋЩчЛсЕФЙуЗКЙизЂЃЌЮЊСЫНтФГЪаГѕжаБЯвЕФъМЖ5 000УћбЇЩњЕФЪгСІЧщПіЃЌЮвУЧДгжаГщШЁСЫвЛВПЗжбЇЩњЕФЪгСІзїЮЊбљБОНјааЪ§ОнДІРэЃЌЕУЕНШчЯТЕФВЛЭъећЕФЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМЃК
ЧыИљОнвдЩЯЭМБэаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉдкЦЕЪ§ЗжВМБэжаЃЌa=________,b=________ЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєЪгСІдк4.6вдЩЯЃЈКЌ4.6ЃЉОљЪєе§ГЃЃЌИљОнЩЯЪіаХЯЂЙРМЦШЋЧјГѕжаБЯвЕЩњжаЪгСІе§ГЃЕФбЇЩњгаЖрЩйЃП
ЁОД№АИЁП 60 0.05
ЁОНтЮіЁП
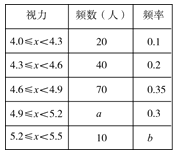
ЃЈ1ЃЉгЩЦЕЪ§ЗжВМБэжадкЕФаХЯЂПЩжЊЃКЪгСІдк4.0ЁмxЃМ4.3ЕФШЫЪ§ЮЊ20ЃЌЦЕТЪЮЊ0.1ЃЌгЩДЫМДПЩЕУЕНБЛГщВщЕФбЇЩњзмЪ§ЮЊЃК20ЁТ0.1=200ЃЈШЫЃЉЃЌетбљгЩ200ЁС0.3ПЩЕУaЃЌгЩ10ЁТ200ПЩЕУbЃЛ
ЃЈ2ЃЉИљОнЃЈ1ЃЉЫљЕУaЕФжЕЃЌНЋЬѕаЮЭГМЦЭМВЙГфЭъећМДПЩЃЛ
ЃЈ3ЃЉИљОнЬтвтНЋЪгСІдк4.6МАвдЩЯЕФШ§зщЪ§ОнЕФЦЕТЪЯрМгЃЌдйНЋЫљЕУЕФКЭгы5000ЯрГЫМДПЩЕУЕНЫљЧѓЕФжЕ.
ЃЈ1ЃЉгЩЦЕЪ§ЗжВМБэжЊЃЌЪгСІдк4.0ЁмxЃМ4.3ЕФШЫЪ§ЮЊ20ЃЌЦЕТЪЮЊ0.1ЃЌ
ЁрДЫДЮЕїВщЕФзмШЫЪ§ЮЊ20ЁТ0.1=200ЃЌ
Ёрa=200ЁС0.3=60ЃЌb=10ЁТ200=0.05ЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊa=60ЃЌдђВЙШЋЬѕаЮЭГМЦЭМШчЯТЃК
ЃЈ3ЃЉгЩЬтвтПЩЕУЃК5 000(0.35+0.3+0.05)=3500ЃЈШЫЃЉ.
Д№ЃКЙРМЦШЋЪаОХФъМЖбЇЩњжаЪгСІе§ГЃЕФга3500ШЫ.


 ЬиИпМЖНЬЪІЕуВІЯЕСаД№АИ
ЬиИпМЖНЬЪІЕуВІЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЁЂBЁЂCШ§ЕудквЛЬѕжБЯпЩЯЃЌИљОнЭМаЮЬюПеЃК
ЃЈ1ЃЉACЃНЁЁ ЁЁ+ЁЁ ЁЁ+ЁЁ ЁЁЃЛ
ЃЈ2ЃЉABЃНACЉЁЁ ЁЁЃЛ
ЃЈ3ЃЉDB+BCЃНЁЁ ЁЁЉAD
ЃЈ4ЃЉШєACЃН8cmЃЌDЪЧЯпЖЮACжаЕуЃЌBЪЧЯпЖЮDCжаЕуЃЌЧѓЯпЖЮABЕФГЄЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁмјдквЛеХжНЩЯЛвЛЬѕЪ§жсЃЌВЂдкЪ§жсЩЯБъГі![]() ЁЂ
ЁЂ![]() СНИіЕуЃЌЕу
СНИіЕуЃЌЕу![]() БэЪОЕФЪ§ЪЧ
БэЪОЕФЪ§ЪЧ![]() ЃЌЕу
ЃЌЕу![]() БэЪОЕФЪ§ЪЧ12ЃЎ
БэЪОЕФЪ§ЪЧ12ЃЎ
ЃЈ1ЃЉШєЪ§жсЩЯЕу![]() гыЕу
гыЕу![]() ЯрОр3ИіЕЅЮЛГЄЖШЃЌЧѓЕу
ЯрОр3ИіЕЅЮЛГЄЖШЃЌЧѓЕу![]() ЫљБэЪОЕФЪ§ЃЛ
ЫљБэЪОЕФЪ§ЃЛ
ЃЈ2ЃЉНЋетеХжНЖделЃЌЪЙЕу![]() гыЕу
гыЕу![]() ИеКУжиКЯЃЌелКлгыЪ§жсНЛгкЕу
ИеКУжиКЯЃЌелКлгыЪ§жсНЛгкЕу![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() БэЪОЕФЪ§ЃЛ
БэЪОЕФЪ§ЃЛ
ЃЈ3ЃЉЕу![]() КЭЕу
КЭЕу![]() ЭЌЪБДгГѕЪМЮЛжУбиЪ§жсЯђзѓдЫЖЏЃЌЕу
ЭЌЪБДгГѕЪМЮЛжУбиЪ§жсЯђзѓдЫЖЏЃЌЕу![]() ЕФЫйЖШЪЧУПУы1ИіЕЅЮЛГЄЖШЃЌЕу
ЕФЫйЖШЪЧУПУы1ИіЕЅЮЛГЄЖШЃЌЕу![]() ЕФЫйЖШЪЧУПУы2ИіЕЅЮЛГЄЖШЃЌдЫЖЏЪБМфЪЧ
ЕФЫйЖШЪЧУПУы2ИіЕЅЮЛГЄЖШЃЌдЫЖЏЪБМфЪЧ![]() Уы.ЪЧЗёДцдк
Уы.ЪЧЗёДцдк![]() ЕФжЕЃЌЪЙ
ЕФжЕЃЌЪЙ![]() УыКѓЕу
УыКѓЕу![]() ЕНдЕуЕФОрРыЕШгкЕу
ЕНдЕуЕФОрРыЕШгкЕу![]() ЕНдЕуЕФОрРыЕФСНБЖЃПШєДцдкЃЌЧыЧѓГі
ЕНдЕуЕФОрРыЕФСНБЖЃПШєДцдкЃЌЧыЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПВйГЁЩЯгавЛИљЪњжБСЂдкЕиУцЩЯЕФЦьИЫЃЌЩўзгздШЛЯТДЙЕНЕиУцЛЙЪЃгр2УзЃЌЕБАбЩўзгРПЊ8УзКѓЃЌЩўзгИеКУаБзХРжБЯТЖЫНгДЅЕиУцЃЈШчЭМЂйЃЉ
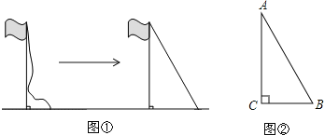
ЃЈ1ЃЉЧыИљОнФуЕФдФЖСРэНтЃЌНЋЬтФПЕФЬѕМўВЙГфЭъећЃКШчЭМЂкЃЌRtЁїABCжа ЁЯC=90ЁуЃЌBC=8УзЃЌ____________________________.ЧѓACЕФГЄЃЎ
ЃЈ2ЃЉИљОнЃЈ1ЃЉжаЕФЬѕМўЃЌЧѓГіЦьИЫЕФИпЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЙъЭУЪзДЮШќХмЁБжЎКѓЃЌЪфСЫБШШќЕФЭУзгУЛгаЦјФйЃЌзмНсЗДЫМКѓЃЌКЭЮкЙъдМЖЈдйШќвЛГЁЃЎЭМжаЕФКЏЪ§ЭМЯѓПЬЛСЫЁАЙъЭУдйДЮШќХмЁБЕФЙЪЪТЃЈxБэЪОЮкЙъДгЦ№ЕуГіЗЂЫљааЕФЪБМфЃЌy1БэЪОЮкЙъЫљааЕФТЗГЬЃЌy2БэЪОЭУзгЫљааЕФТЗГЬЃЉЃЎгаЯТСаЫЕЗЈЃК
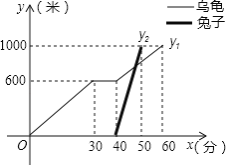
ЂйЁАЙъЭУдйДЮШќХмЁБЕФТЗГЬЮЊ1000УзЃЛ
ЂкЭУзгКЭЮкЙъЭЌЪБДгЦ№ЕуГіЗЂЃЛ
ЂлЮкЙъдкЭОжаанЯЂСЫ10ЗжжгЃЛ
ЂмЭУзгдкЭОжа750УзДІзЗЩЯЮкЙъЃЎ
Цфжае§ШЗЕФЫЕЗЈЪЧЁЁ ЁЁЃЎЃЈАбФуШЯЮЊе§ШЗЫЕЗЈЕФађКХЖМЬюЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABEКЭЁїADCЪЧЁїABCЗжБ№бизХABЁЂACБпЗел180ЁуаЮГЩЕФЃЌШєЁЯ1ЃКЁЯ2ЃКЁЯ3=28ЃК5ЃК3ЃЌдђЁЯІСЕФЖШЪ§ЮЊ__ЖШЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФЃаЭНщЩмЃКЙХЯЃРАгавЛИіжјУћЕФЁАНЋОќвћТэЮЪЬтЁБЃЌДѓжТФкШнШчЯТЃКЙХЯЃРАвЛЮЛНЋОќЃЌУПЬьЖМвЊбВВщКгАЖВрЕФСНИіОќгЊAЁЂBЃЌЫћзмЪЧЯШШЅAгЊЃЌдйЕНКгБпвћТэЃЌжЎКѓдйШЅBгЊЃЌШчЭМЂйЃЌЫћЪБГЃЯыЃЌдѕУДзпВХФмЪЙУПЬьЕФТЗГЬжЎКЭзюЖЬФиЃП
ДѓЪ§бЇМвКЃТздјгУжсЖдГЦЕФЗНЗЈЧЩУюЕФНтОіСЫетЮЪЬт.
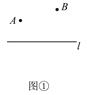
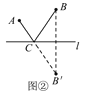
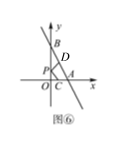
ШчЭМЂкЃЌзїBЙигкжБЯпlЕФЖдГЦЕуBЁфЃЌСЌНгABЁфгыжБЯпlНЛгкЕуCЃЌЕуCОЭЪЧЫљЧѓЕФЮЛжУЃЎ
ЧыФудкЯТСаЕФдФЖСЁЂгІгУЕФЙ§ГЬжаЃЌЭъГЩНтД№ЃЎ
ЃЈ1ЃЉРэгЩЃКШчЭМЂлЃЌдкжБЯпlЩЯСэШЁШЮвЛЕуCЁфЃЌСЌНгACЁфЃЌBCЁфЃЌBЁфCЁфЃЌ
ЁпжБЯпlЪЧЕуBЃЌBЁфЕФЖдГЦжсЃЌЕуCЃЌCЁфдкlЩЯЃЌ
ЁрCB=_______ЃЌCЁфB=_______.
ЁрAC+CB=AC+CBЁф=_______ЃЎ
дкЁїACЁфBЁфжаЃЌЁпABЁфЃМACЁф+CЁфBЁфЃЌЁрAC+CBЃМACЁф+CЁфBЁфЃЌМДAC+CBзюаЁ.
ЙщФЩаЁНсЃК
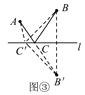
БОЮЪЬтЪЕМЪЪЧРћгУжсЖдГЦБфЛЛЕФЫМЯыЃЌАбAЁЂBдкжБЯпЕФЭЌВрЮЪЬтзЊЛЏЮЊдкжБЯпЕФСНВрЃЌДгЖјПЩРћгУЁАСНЕужЎМфЯпЖЮзюЖЬЁБЃЌМДзЊЛЏЮЊЁАШ§НЧаЮСНБпжЎКЭДѓгкЕкШ§БпЁБЕФЮЪЬтМгвдНтОіЃЈЦфжаCЮЊABЁфгыlЕФНЛЕуЃЌМДAЁЂCЁЂBЁфШ§ЕуЙВЯпЃЉЃЎ
БОЮЪЬтПЩЭиеЙЮЊЁАЧѓЖЈжБЯпЩЯвЛЖЏЕугыжБЯпЭтСНЖЈЕуЕФОрРыКЭЕФзюаЁжЕЁБЮЪЬтЕФЪ§бЇФЃаЭЃЎ
ЃЈ2ЃЉФЃаЭгІгУ
ЂйШчЭМ ЂмЃЌе§ЗНаЮABCDЕФБпГЄЮЊ2ЃЌEЮЊABЕФжаЕуЃЌFЪЧACЩЯвЛЖЏЕуЃЌЧѓEF+FBЕФзюаЁжЕ.
НтОіетИіЮЪЬтЃЌПЩвдНшжњЩЯУцЕФФЃаЭЃЌгЩе§ЗНаЮЕФЖдГЦадПЩжЊЃЌBгыDЙигкжБЯпACЖдГЦЃЌСЌНгEDНЛACгкFЃЌдђEF+FBЕФзюаЁжЕОЭЪЧЯпЖЮDEЕФГЄЖШЃЌEF+FBЕФзюаЁжЕЪЧ_______ЃЎ
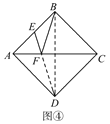
ЂкШчЭМЂнЃЌвбжЊЁбOЕФжБОЖCDЮЊ4ЃЌЁЯAODЕФЖШЪ§ЮЊ60ЁуЃЌЕуBЪЧЛЁADЕФжаЕуЃЌдкжБОЖCDЩЯеввЛЕуPЃЌЪЙBP+APЕФжЕзюаЁЃЌдђBP+APЕФзюаЁжЕЪЧ_______ЃЛ
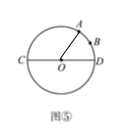
ЂлШчЭМЂоЃЌвЛДЮКЏЪ§y=-2x+4ЕФЭМЯѓгыxЃЌyжсЗжБ№НЛгкAЃЌBСНЕуЃЌЕуOЮЊзјБъдЕуЃЌЕуCгыЕуDЗжБ№ЮЊЯпЖЮOAЃЌABЕФжаЕуЃЌЕуPЮЊOBЩЯвЛЖЏЕуЃЌЧѓPC+PDЕФзюаЁжЕЃЌВЂаДГіШЁЕУзюаЁжЕЪБPЕузјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋГЄЮЊ20cmЃЌПэЮЊ8cmЕФГЄЗНаЮАзжНЃЌАДШчЭМЫљЪОЕФЗНЪНеГКЯЦ№РДЃЌеГКЯВПЗжЕФПэЮЊ3cm.

(1)ИљОнЬтвтЃЌНЋЯТУцЕФБэИёВЙГфЭъећ.
АзжНеХЪ§x(еХ) | 1 | 2 | 3 | 4 | 5 | Ё |
жНЬѕзмГЄЖШy(cm) | 20 | 54 | 71 | Ё |
ЃЈ2ЃЉжБНгаДГіyгыxЕФЙиЯЕЪН.
(3ЃЉвЊЪЙеГКЯКѓЕФГЄЗНаЮзмУцЛ§ЮЊ1656cm2ЃЌдђашгУЖрЩйеХетбљЕФАзжН?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЪ§бЇПЮБОжаЃЌгаетбљвЛЕРЬтЃКвбжЊЃКШчЃЈЭМ1ЃЉЃЌЁЯB+ЁЯCЃНЁЯBECЧѓжЄЃКABЁЮCD
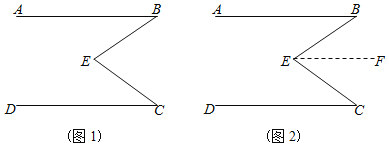
ЃЈ1ЃЉЧыВЙГфЯТУцжЄУїЙ§ГЬ
жЄУїЃКЙ§ЕуEЃЌзіEFЁЮABЃЌШчЃЈЭМ2ЃЉ
ЁрЁЯBЃНЁЯЁЁ ЁЁ
ЁпЁЯB+ЁЯCЃНЁЯBECЁЯBEF+ЁЯFECЃНЁЯBECЃЈвбжЊЃЉ
ЁрЁЯB+ЁЯCЃНЁЯBEF+ЁЯFECЃЈЕШСПДњЛЛЃЉ
ЁрЁЯЁЁ ЁЁЃНЁЯЁЁ ЁЁЃЈЕШЪНаджЪЃЉ
ЁрEFЁЮЁЁ ЁЁ
ЁпEFЁЮAB
ЁрABЁЮCDЃЈЦНаагкЭЌвЛЬѕжБЯпЕФСНЬѕжБЯпЛЅЯрЦНааЃЉ
ЃЈ2ЃЉЧыдйбЁгУвЛжжЗНЗЈЃЌМгвджЄУї
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com