
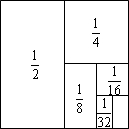
 如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形,接着把一个面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$的矩形…如此进行下去.
如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形,接着把一个面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$的矩形…如此进行下去.分析 (1)分析图形中的数据可知:$\frac{1}{2}=1-\frac{1}{2}$,$\frac{1}{2}+\frac{1}{4}=1-\frac{1}{4}$,$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=1-\frac{1}{8}$,以此类推可得结论;
(2)由(1)类比可得规律为:$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…\frac{1}{{2}^{n}}=1-\frac{1}{{2}^{n}}$.
解答 解:(1)分析图形中的数据可知:$\frac{1}{2}=1-\frac{1}{2}$,$\frac{1}{2}+\frac{1}{4}=1-\frac{1}{4}$,$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=1-\frac{1}{8}$,以此类推,$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$+$\frac{1}{256}$=1-$\frac{1}{256}$=$\frac{255}{256}$;
故答案为:$\frac{255}{256}$.
(2)由(1)类比可得规律为:$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…\frac{1}{{2}^{n}}=1-\frac{1}{{2}^{n}}$.
点评 本题考查了根据图形探索规律问题,此题注意每次分割都是分两份,求若干个矩形的面积和也可以换个方法思考,用减法简单地计算出来.


科目:初中数学 来源: 题型:解答题
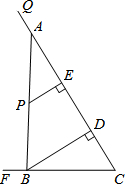 如图,tan∠QCF=2,点E在射线CQ上,CE=12.点P是∠QCF内一点,PE⊥QC于点E,PE=4.在射线CQ上取一点A,连AP并延长交射线CF于点B,作BD⊥QC于点D.
如图,tan∠QCF=2,点E在射线CQ上,CE=12.点P是∠QCF内一点,PE⊥QC于点E,PE=4.在射线CQ上取一点A,连AP并延长交射线CF于点B,作BD⊥QC于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
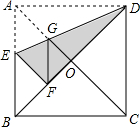 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形ABCD使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=122.5°;②$\frac{AD}{AE}=2$;③BE=2OG;④DG=2EG;⑤AC-AD=EF,其中正确的序号是( )
如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形ABCD使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=122.5°;②$\frac{AD}{AE}=2$;③BE=2OG;④DG=2EG;⑤AC-AD=EF,其中正确的序号是( )| A. | ①③⑤ | B. | ①②③ | C. | ③④ | D. | ③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 工种 属地 | 钳工 | 车工 |
| A地 | 1800(元/月) | 1600(元/月) |
| B地 | 1600(元/月) | 1200(元/月) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
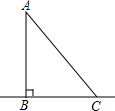 某小区的A处有一个凉亭,道路AB、BC、AC两两相交于点A、B、C,并且道路AB与道路BC相互垂直.如图所示,已知A和B之间的距离为20m,若有两个小朋友在与点B相距10m点D处玩耍,玩累了他们沿不同的路线到凉亭A处喝水休息,已知D→B→A与D→C→A的路程相等,求A与C之间的距离.
某小区的A处有一个凉亭,道路AB、BC、AC两两相交于点A、B、C,并且道路AB与道路BC相互垂直.如图所示,已知A和B之间的距离为20m,若有两个小朋友在与点B相距10m点D处玩耍,玩累了他们沿不同的路线到凉亭A处喝水休息,已知D→B→A与D→C→A的路程相等,求A与C之间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com