
分析 首先求出x1,x2,x3,x4,x5,x6,…,判断出x1,x2,x3,…xk中,按照1,2,3,4,1,2,3,4,…,每4个数一个循环;然后用2015除以4,根据商和余数的情况,判断出x2015是第几个循环的第几个数,进而判断出x2015等于多少即可.
解答 解:∵x1=1,
∴x2=x1+1-4([$\frac{2-1}{4}$]-[$\frac{2-2}{4}$])=1+1-4×0=2,
∵x2=2,
∴x3=x2+1-4([$\frac{3-1}{4}$]-[$\frac{3-2}{4}$])=2+1-4×0=3,
∵x3=3,
∴x4=x3+1-4([$\frac{4-1}{4}$]-[$\frac{4-2}{4}$])=3+1-4×0=4,
∵x4=4,
∴x5=x4+1-4([$\frac{5-1}{4}$]-[$\frac{5-2}{4}$])=4+1-4×1=1,
∵x5=1,
∴x6=x5+1-4([$\frac{6-1}{4}$]-[$\frac{6-2}{4}$])=1+1-4×0=2,
…,
∴x1,x2,x3,…xk中,按照1,2,3,4,1,2,3,4,…,每4个数一个循环,
∵2015÷4=503…3,
∴x2015是第504个循环的第3个数,
∴x2015=3.
故答案为:3.
点评 此题主要考查了规律型:数字的变化类问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:x1,x2,x3,…xk中,按照1,2,3,4,1,2,3,4,…,每4个数一个循环.


科目:初中数学 来源: 题型:解答题
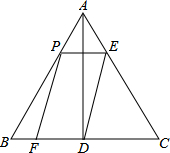 如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连结ED,以PE、ED为邻边作?PEDF.设?PEDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6).
如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连结ED,以PE、ED为邻边作?PEDF.设?PEDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
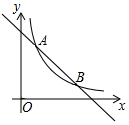 如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
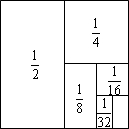 如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形,接着把一个面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$的矩形…如此进行下去.
如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形,接着把一个面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$的矩形…如此进行下去.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
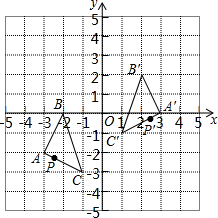 如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )| A. | (-a,b-2) | B. | (-a,b+2) | C. | (-a+2,-b) | D. | (-a+2,b+2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25米 | B. | 50米 | C. | 25$\sqrt{3}$米 | D. | 50$\sqrt{3}$米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com