
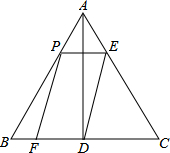
 ��ͼ���ڵȱߡ�ABC�У�AB=6��AD��BC�ڵ�D����P�ڱ�AB���˶�������P��PE��BC�����AC���ڵ�E������ED����PE��EDΪ�ڱ���?PEDF����?PEDF���ABC�ص�����ͼ�ε����Ϊy���߶�AP�ij�Ϊx��0��x��6����
��ͼ���ڵȱߡ�ABC�У�AB=6��AD��BC�ڵ�D����P�ڱ�AB���˶�������P��PE��BC�����AC���ڵ�E������ED����PE��EDΪ�ڱ���?PEDF����?PEDF���ABC�ص�����ͼ�ε����Ϊy���߶�AP�ij�Ϊx��0��x��6�������� ��1��֤����APE�ǵȱ������Σ�������⣻
��2���ı���PEDFΪ����ʱ��AE=DE��Ȼ��֤��DE=EC���ɵõ�E��AC���е㣬��P��AB���е㣬�ݴ˼�����⣻
��3����x=3����P��AB���е�ʱ��PE=$\frac{1}{2}$BC����F��B�غϣ���0��x��3ʱ���غϲ��־���ƽ���ı���PEDF����3��x��6ʱ���غϲ���������PEDB������ƽ���ı��κ����ε������ʽ������⣻
��4��������õ�A'B���д������þ�����Dʱx��ֵ���ݴ˼�����⣮
��� �⣺��1����PE��BC��
���APE�ס�ABC��
�֡ߡ�ABC�ǵȱߡ���
���APE�ǵȱ������Σ�
��PE=AP=x��0��x��6����
��2�����ı���PEDFΪ���Σ�
��PE=DE=x��
�֡ߡ�APE�ǵȱ������Σ���AE=PE��
��AE=DE��
���DAC=��ADE��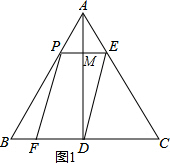
�֡ߡ�ADE+��EDC=��DAC+��C=90�㣬
���EDC=��C��
��DE=EC��
��DE=EC=AE=$\frac{1}{2}$AC=$\frac{1}{2}$AB=3��
��x=3��
��3����x=3����P��AB���е�ʱ��PE=$\frac{1}{2}$BC����F��B�غϣ�
��0��x��3ʱ���غϲ��־���ƽ���ı���PEDF����ͼ1��
�ȱߡ�ABC�У�AD=AB•sin60��=6��$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$���ȱߡ�APE�У�AM=AP•sin60��=$\frac{\sqrt{3}}{2}$x��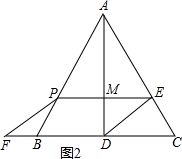
��DM=3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x��
��y=x��3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x������y=-$\frac{\sqrt{3}}{2}$x2+3$\sqrt{3}$x��
��3��x��6ʱ���غϲ���������PEDB����ͼ2��
��y=$\frac{1}{2}$��PE+BD��•DM=$\frac{1}{2}$��x+3��•��3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x������y=-$\frac{\sqrt{3}}{4}{x}^{2}+\frac{3\sqrt{3}}{4}x+\frac{9\sqrt{3}}{2}$��
��4������һ����A����BC�Ϸ�ʱ����ͼ3��ʾ��
��A��B���д������þ�����Dʱ��A��D=BD=3��
��AA��=3$\sqrt{3}$-3��
��AM=$\frac{1}{2}$AA��=$\frac{1}{2}$��3$\sqrt{3}$-3����
��x=AP=$\frac{\frac{1}{2}��3\sqrt{3}-3��}{\frac{\sqrt{3}}{2}}$=3-$\sqrt{3}$��
��x��ȡֵ��Χ�ǣ�0��x��3-$\sqrt{3}$��
���ζ�����A����BC��ʱ��PQ��AD����ͼ4��ʾ��
AP=A��P=BP=$\frac{1}{2}$AB=$\frac{1}{2}$��6=3��
����������A����BC�·�ʱ����ͼ5��ʾ��
��A��B���д������þ�����Dʱ��A��D=BD=3��
��AA��=3$\sqrt{3}$+3��
��AM=$\frac{1}{2}$AA��=$\frac{1}{2}$��3$\sqrt{3}$+3����
��x=AP=$\frac{\frac{1}{2}��3\sqrt{3}+3��}{\frac{\sqrt{3}}{2}}$=3+$\sqrt{3}$��
��x��ȡֵ��Χ�ǣ�3��x��3+$\sqrt{3}$��
������ʾ��x��ȡֵ��ΧΪ0��x��3-$\sqrt{3}$��3��x��3+$\sqrt{3}$��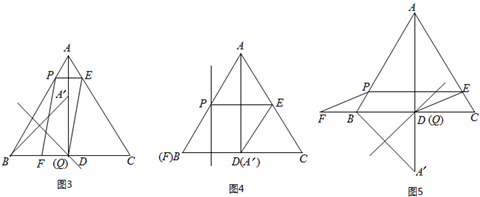
���� �����ǵȱ������ε������Լ����ε����ʵ��ۺ�Ӧ�ã����F��B�غ��Լ�A'B���д������þ�����Dʱ�����������t��ֵ�ǹؼ���


 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
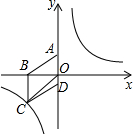 ��ͼ��������ABCD������ƽ��ֱ������ϵ�У���֪A��0��3����B��-4��0��
��ͼ��������ABCD������ƽ��ֱ������ϵ�У���֪A��0��3����B��-4��0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
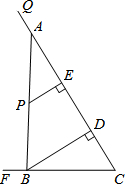 ��ͼ��tan��QCF=2����E������CQ�ϣ�CE=12����P�ǡ�QCF��һ�㣬PE��QC�ڵ�E��PE=4��������CQ��ȡһ��A����AP���ӳ�������CF�ڵ�B����BD��QC�ڵ�D��
��ͼ��tan��QCF=2����E������CQ�ϣ�CE=12����P�ǡ�QCF��һ�㣬PE��QC�ڵ�E��PE=4��������CQ��ȡһ��A����AP���ӳ�������CF�ڵ�B����BD��QC�ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
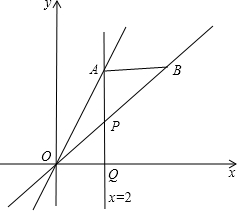 ��֪��ֱ��y=2x��x=2�ཻ�ڵ�A��ֱ��x=2��x���ཻ�ڵ�Q����P������AQ�ϵ�һ�㣬��B��ֱ��OP�ϵ�һ�㣬��AP=t����B������Ϊ��a��b����
��֪��ֱ��y=2x��x=2�ཻ�ڵ�A��ֱ��x=2��x���ཻ�ڵ�Q����P������AQ�ϵ�һ�㣬��B��ֱ��OP�ϵ�һ�㣬��AP=t����B������Ϊ��a��b�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��-2��x��-1 | B�� | x��-2��x��-1 | C�� | x��2��x��-1 | D�� | x��2��x��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 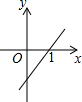 | B�� | 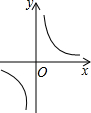 | C�� | 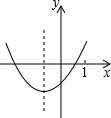 | D�� | 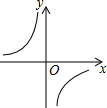 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com