
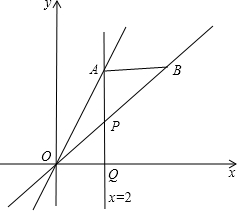
 ��֪��ֱ��y=2x��x=2�ཻ�ڵ�A��ֱ��x=2��x���ཻ�ڵ�Q����P������AQ�ϵ�һ�㣬��B��ֱ��OP�ϵ�һ�㣬��AP=t����B������Ϊ��a��b����
��֪��ֱ��y=2x��x=2�ཻ�ڵ�A��ֱ��x=2��x���ཻ�ڵ�Q����P������AQ�ϵ�һ�㣬��B��ֱ��OP�ϵ�һ�㣬��AP=t����B������Ϊ��a��b�������� ��1�����������A����P��������Ƕ��٣�Ȼ����ݴ���ϵ���������ֱ��OP�Ľ���ʽ���ɣ�
��2�����ȸ��������������ж��ķ������жϳ���BDA�ס�ACO�������жϳ�DA=2BD��Ȼ�����a-2=2��[4-$\frac{��4-t��a}{2}$]�����a��t֮��Ĺ�ϵʽ���ɣ�
��3���������⣬��3�������������A����x����������ʱ��������A����x�Ḻ������ʱ��������A����y�Ḻ������ʱ���������ۣ��������������������t��ֵ����д����A��A�䣬P��BΪ������ı���Ϊ����ʱ�ĵ�B���꼴�ɣ�
��� �⣺��1����x=2ʱ��y=2x=4��
���A��������2��4����
��AP=t��
���P��������2��4-t��
��ֱ��OP�Ľ���ʽΪy=kx��
��x=2��y=4-t������ʽ��
�ɵ�4-t=2k��
���k=$\frac{4-t}{2}$��
��y=$\frac{4-t}{2}$x��
��2����ͼ1����A��CD��y���ڵ�C��BD��CD�ڵ�D��
��ֱ��OP�Ľ���ʽ��y=$\frac{4-t}{2}$x��
���B��a��$\frac{��4-t��a}{2}$������D��a��4����
��DA=a-2��BD=4-$\frac{��4-t��a}{2}$��
����BAO=90��ʱ��
�ߡ�DAB+��CAO=90�㣬��COA+��CAO=90�㣬
���DAB=��COA��
���BDA�ס�ACO��
��$\frac{BD}{AC}=\frac{DA}{CO}$��
��$\frac{BD}{DA}=\frac{AC}{CO}=\frac{2}{4}=\frac{1}{2}$��
��DA=2BD��
��a-2=2��[4-$\frac{��4-t��a}{2}$]��
���a=$\frac{10}{5-t}$��0��t��5����
��3������ͼ2������A����x���������ϣ�
���ı���AA��PBΪ���Σ�
��BA���AQ��AQ��x�ᣬ
��BA���x�ᣬ
�ߵ�A���A�����ֱ��PB�Գƣ�
��OA��=OA=$\sqrt{{2}^{2}{+4}^{2}}=2\sqrt{5}$��
��A��Q=2$\sqrt{5}$-2��
���ı���AA��PBΪ���Σ�
��PA��=AP=t��
��Rt��PQA����
PQ2+A��Q2=PA��2��
�ࣨ4-t��2+��2$\sqrt{5}$-2��2=t2��
���t=5-$\sqrt{5}$��
��ʱֱ��OP�Ľ���ʽ�ǣ�
y=$\frac{4-t}{2}$x=$\frac{4-��5-\sqrt{5}��}{2}$x=$\frac{\sqrt{5}-1}{2}x$��
��x=2$\sqrt{5}$ʱ��
y=$\frac{\sqrt{5}-1}{2}��2\sqrt{5}=5-\sqrt{5}$��
���B������2$\sqrt{5}$��5-$\sqrt{5}$����
����ͼ3������A����y�Ḻ�����ϣ�����AA�佻OB��E�� ��
��
���ı���AA��PBΪ���Σ�
��BA���AQ��AQ��x�ᣬ
��BA���x�ᣬ
�ߵ�A���A�����ֱ��PB�Գƣ�
��OA��=OA=$\sqrt{{2}^{2}{+4}^{2}}=2\sqrt{5}$��
��A��Q=2$\sqrt{5}$+2��
���ı���AA��PBΪ���Σ�
��PA��=AP=t��
��Rt��PQA����
PQ2+A��Q2=PA��2��
�ࣨt-4��2+��2$\sqrt{5}$+2��2=t2��
���t=5+$\sqrt{5}$��
��ʱֱ��OP�Ľ���ʽ�ǣ�
y=$\frac{4-t}{2}$x=$\frac{4-��5+\sqrt{5}��}{2}$x=$-\frac{\sqrt{5}+1}{2}x$��
��x=-2$\sqrt{5}$ʱ��
y=-$-\frac{\sqrt{5}+1}{2}$��$��-2\sqrt{5}��$=5$+\sqrt{5}$��
���B������-2$\sqrt{5}$��5+$\sqrt{5}$����
����ͼ4������A����x�Ḻ�����ϣ�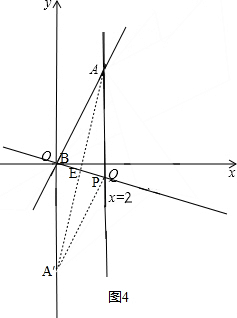
���ı���AA��PBΪ���Σ�
��BA���AQ��AQ��x�ᣬ
��BA���x�ᣬ
�ߵ�A���A�����ֱ��PB�Գƣ�
��OA��=OA=$\sqrt{{2}^{2}{+4}^{2}}=2\sqrt{5}$��
��t=2$\sqrt{5}$ʱ��
OA=OA��=A��P=AP=2$\sqrt{5}$��
��ʱ��B����Ϊ��0��0����
���ϣ��ɵ�
��t=5-$\sqrt{5}$ʱ����B����Ϊ��2$\sqrt{5}$��5-$\sqrt{5}$����
��t=5+$\sqrt{5}$ʱ����B����Ϊ��-2$\sqrt{5}$��5+$\sqrt{5}$����
��t=2$\sqrt{5}$ʱ����B����Ϊ��0��0����
���� ��1��������Ҫ������һ�κ����ۺ��⣬�����˷������������������˷�������˼���Ӧ�ã����������ν��˼���Ӧ�ã������˴���֪����ͼ���л�ȡ��Ϣ���������û�ȡ����Ϣ�����Ӧ�������������
��2�����������ȫ�������ε��ж������ʵ�Ӧ�ã��Լ����������ε��ж������ʵ�Ӧ�ã�Ҫ�������գ�
��3����������˴���ϵ�������ֱ�ߵĽ���ʽ���⣬Ҫ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
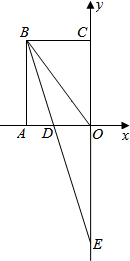 ������ABCO��ͼ������ƽ��ֱ������ϵ�У���ABO��ƽ����BE��x���ڵ�D����y���ڵ�E���߶�OA��OC��OA��OC���ij���һԪ���η���x2-21x+108=0���������������������⣺
������ABCO��ͼ������ƽ��ֱ������ϵ�У���ABO��ƽ����BE��x���ڵ�D����y���ڵ�E���߶�OA��OC��OA��OC���ij���һԪ���η���x2-21x+108=0���������������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
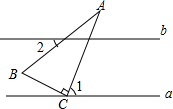 ��ͼ��ֱ��a��b��������30��ǵ����ǰ�ABC��ֱ�Ƕ���C����ֱ��a�ϣ�����1=65�㣬���2�Ķ���Ϊ��������
��ͼ��ֱ��a��b��������30��ǵ����ǰ�ABC��ֱ�Ƕ���C����ֱ��a�ϣ�����1=65�㣬���2�Ķ���Ϊ��������| A�� | 25�� | B�� | 30�� | C�� | 35�� | D�� | 40�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2.5��1��3 | B�� | 2��1 | C�� | 3��1 | D�� | 2.5��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
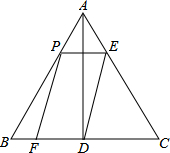 ��ͼ���ڵȱߡ�ABC�У�AB=6��AD��BC�ڵ�D����P�ڱ�AB���˶�������P��PE��BC�����AC���ڵ�E������ED����PE��EDΪ�ڱ���?PEDF����?PEDF���ABC�ص�����ͼ�ε����Ϊy���߶�AP�ij�Ϊx��0��x��6����
��ͼ���ڵȱߡ�ABC�У�AB=6��AD��BC�ڵ�D����P�ڱ�AB���˶�������P��PE��BC�����AC���ڵ�E������ED����PE��EDΪ�ڱ���?PEDF����?PEDF���ABC�ص�����ͼ�ε����Ϊy���߶�AP�ij�Ϊx��0��x��6�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com