【题目】如图，在四边形ABCD中，对角线AC与BD相交于点O，不能判断四边形ABCD是平行四边形的是（ ）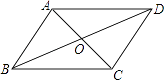 
A.AB∥DC，AD=BC
B.AB∥DC，AD∥BC
C.AB=DC，AD=BC
D.OA=OC，OB=OD
科目：初中数学 来源： 题型：
【题目】点A、B在数轴上分别表示实数
、
，A、B两点之间的距离记作AB.
当A、B两点中有一点为原点时，不妨设A点在原点.如图①所示，则AB＝OB＝
＝
．
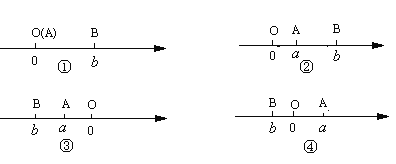
当A、B两点都不在原点时：
(1)如图②所示，点A、B都在原点的右边，不妨设点A在点B的左侧，则AB＝OB－OA＝
＝
＝
＝
(2)如图③所示，点A、B都在原点的左边，不妨设点A在点B的右侧，则AB＝OB－OA＝
＝
＝
＝
(3)如图④所示，点A、B分别在原点的两边，不妨设点A在点O的右侧，则AB＝OB＋OA＝
＝
＝
回答下列问题：
(1)综上所述，数轴上A、B两点之间的距离AB＝ ．
(2)数轴上表示2和－4的两点A和B之间的距离AB＝ ．
(3)数轴上表示
和－2的两点A和B之间的距离AB＝ ，如果AB＝2，则
的值为 ．
(4)若代数式
有最小值，则最小值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．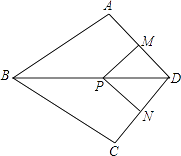 
（1）求证：∠ADB=∠CDB；
（2）若∠ADC=90°，求证：四边形MPND是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
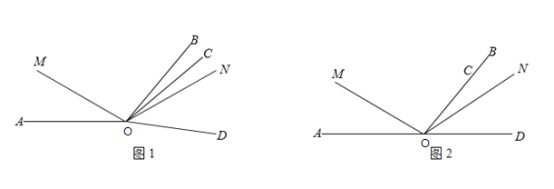
【题目】如图1，已知∠AOB＝120°，∠COD＝60°，OM在∠AOC内，ON在∠BOD内，∠AOM＝
∠AOC，∠BON＝
∠BOD．
（1）∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时，如图2，∠MON＝ °；
（2）∠COD从图2中的位置绕点O逆时针旋转n°（0＜n＜120且n≠60），求∠MON的度数；
（3）∠COD从图2中的位置绕点O逆时针旋转n°（0＜n＜120），则n＝ 时，∠MON＝2∠BOC．
查看答案和解析>>
科目：初中数学 来源： 题型：
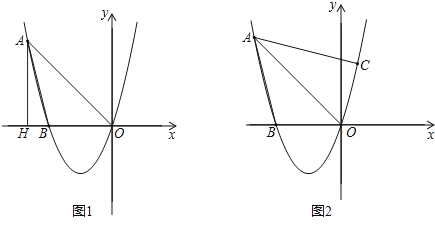
【题目】已知，经过点A（－4，4）的抛物线y=ax2+bx+c与x轴相交于点B（－3，0）及原点O．
（1）求抛物线的解析式；
（2）如图1，过点A作AH⊥x轴，垂足为H，平行于y轴的直线交线段AO于点Q，交抛物线于点P，当四边形AHPQ为平行四边形时，求∠AOP的度数；
（3）如图2，若点C在抛物线上，且∠CAO＝∠BAO，试探究：在（2）的条件下，是否存在点G，使得△GOP∽△COA？若存在，请求出所有满足条件的点G坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
