
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N. 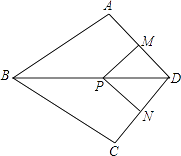
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
【答案】
(1)证明:∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
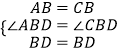 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB
(2)证明:∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
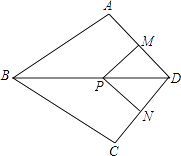
【解析】(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.
【考点精析】根据题目的已知条件,利用正方形的判定方法的相关知识可以得到问题的答案,需要掌握先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角.


科目:初中数学 来源: 题型:
【题目】在“低碳生活,绿色出行”的倡导下,自行车正逐渐成为人们喜爱的交通工具,运动商城自2018年起自行车的销售量逐月增加.据统计,商城一月份销售自行车64辆,三月份销售了100辆,则运动商城的自行车销量的月平均增长率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
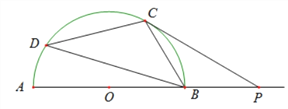
【题目】如图,已知半圆O,AB为直径,P为射线AB上一点,过点P作⊙O的切线,切点为C点,D为弧AC上一点,
连接BD、BC.
(1)求证:∠D=∠PCB;
(2)若四边形CDBP为平行四边形,求∠BPC度数;
(3)若AB=8,PB=2,求PC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C在线段AD上,CD=2AB+3.
(1)若点C是线段AD的中点,求BC-AB的值;
(2)若BC=![]() AD,求BC-AB的值;
AD,求BC-AB的值;
(3)若线段AC上有一点P(不与点B重合),AP+AC=DP,求BP的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( ) 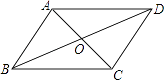
A.AB∥DC,AD=BC
B.AB∥DC,AD∥BC
C.AB=DC,AD=BC
D.OA=OC,OB=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的表达式为( )
A.y=(x+2)2+3
B.y=(x﹣2)2+3
C.y=(x+2)2﹣3
D.y=(x﹣2)2﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
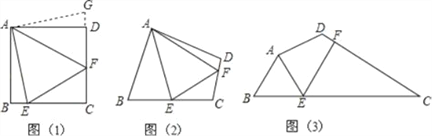
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com