
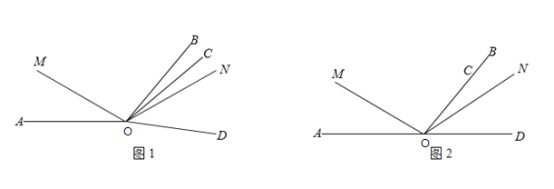
【题目】如图1,已知∠AOB=120°,∠COD=60°,OM在∠AOC内,ON在∠BOD内,∠AOM=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD.
∠BOD.
(1)∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时,如图2,∠MON= °;
(2)∠COD从图2中的位置绕点O逆时针旋转n°(0<n<120且n≠60),求∠MON的度数;
(3)∠COD从图2中的位置绕点O逆时针旋转n°(0<n<120),则n= 时,∠MON=2∠BOC.
【答案】(1)100°;(2)100°;(3)50或70.
【解析】试题分析:(1)由∠MON=![]() ∠AOB+
∠AOB+![]() ∠COD代入即可得到结论;
∠COD代入即可得到结论;
(2)分两种情况讨论:①当0<n<60°时,∠AOC=∠AOB-∠BOC=120°-n,∠BOD=60°-n,由∠MON=∠MOC+∠COB+∠BON,代入即可得到结论;
②当60°<n<120°时,∠AOC=120°-n,∠COD=60°,∠BOD=n-60°,∠MOC=![]() ∠AOC,∠DON=
∠AOC,∠DON=![]() ∠BOD,由∠MON=∠MOC+∠COD+∠DON,代入即可得到结论.
∠BOD,由∠MON=∠MOC+∠COD+∠DON,代入即可得到结论.
(3)分两种情况讨论:①当0<n<60°时,∠BOC=n,∠MON=2n,由∠MON=![]() (120°+n)+60°-
(120°+n)+60°-![]() (60°+n)=100°,解方程即可得到结论;
(60°+n)=100°,解方程即可得到结论;
②当60°<n<120°时,∠AOC=360°-(120°+n)=240°-n,∠BOD=60°+n,由∠MON=360°-∠AOM-∠AOB-∠BON=360°-![]() (240°-n)-120°-
(240°-n)-120°-![]() (60°+n)=140°,解方程即可得到结论.
(60°+n)=140°,解方程即可得到结论.
试题解析:解:(1)∠MON=![]() ∠AOB+
∠AOB+![]() ∠COD=100°;
∠COD=100°;
(2)①当0<n<60°时,∠AOC=∠AOB-∠BOC=120°-n,∠BOD=60°-n,∴∠MON=∠MOC+∠COB+∠BON=![]() ∠AOC+n+
∠AOC+n+![]() ∠BOD=
∠BOD=![]() (120°-n)+n+
(120°-n)+n+![]() (60°-n)=100°;
(60°-n)=100°;

②当60°<n<120°时,∠AOC=120°-n,∠COD=60°,∠BOD=n-60°,∠MOC=![]() ∠AOC,∠DON=
∠AOC,∠DON=![]() ∠BOD,∴∠MON=∠MOC+∠COD+∠DON=
∠BOD,∴∠MON=∠MOC+∠COD+∠DON=![]() (120°-n)+60°+
(120°-n)+60°+![]() (n-60°)=100°.
(n-60°)=100°.

综上所述:∠MON的度数恒为100°.
(3)①当0<n<60°时,∠BOC=n,∠MON=2n,∴∠MON=![]() (120°+n)+60°-
(120°+n)+60°-![]() (60°+n)=100°;解得:n=50°;
(60°+n)=100°;解得:n=50°;

②当60°<n<120°时,∠AOC=360°-(120°+n)=240°-n,∠BOD=60°+n,∴∠MON=360°-∠AOM-∠AOB-∠BON=360°-![]() (240°-n)-120°-
(240°-n)-120°-![]() (60°+n)=140°,解得:n=70°.
(60°+n)=140°,解得:n=70°.

综上所述:n=50°或70°.


科目:初中数学 来源: 题型:
【题目】为解决群众看病贵的问题,有关部门决定降低药价,原价为30元的药品经过连续两次降价,价格变为24.3元,则平均每次降价的百分率为( )
A.10%B.15%C.20%D.25%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C在线段AD上,CD=2AB+3.
(1)若点C是线段AD的中点,求BC-AB的值;
(2)若BC=![]() AD,求BC-AB的值;
AD,求BC-AB的值;
(3)若线段AC上有一点P(不与点B重合),AP+AC=DP,求BP的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( ) 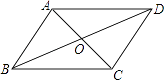
A.AB∥DC,AD=BC
B.AB∥DC,AD∥BC
C.AB=DC,AD=BC
D.OA=OC,OB=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
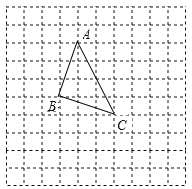
【题目】如图,所有小正方形的边长都为1,A,B,C都在格点上.
(1)过点C画直线AB的平行线CD;
(2)过点B画直线AC的垂线,并注明垂足为G;
(3)△ABC的面积为 ;
(4)线段AB、BG的大小关系为:AB BG,理由是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com