
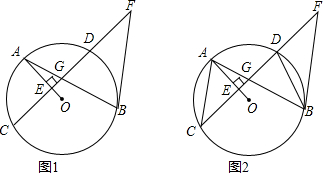
分析 (1)连接OC,OB,若要证明FG=FB,只要转化为证明∠FGB=∠FBG即可;
(2)由已知条件易证∠DGB=∠GDB,因为∠CAB和∠BDC都是弧BC所对的圆周角,所以∠CAB=∠BDC,进而可证明∠CAB=∠GBF,则AC∥BF.
解答 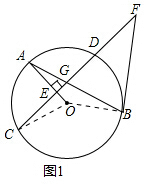 证明:(1)如图1,连接OB,
证明:(1)如图1,连接OB,
∵BF是⊙O的切线,
∴∠OBF=90°,
∴∠OBA+∠GBF=90°,
∵OA⊥CD,
∴∠AEG=90°,
∴∠AGE+∠EAG=90°,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠AGE=∠FBG,
∵∠AGE=∠FGB,
∴∠FGB=∠FBG,
∴FG=FB;
(2)∵BD=BG,
∴∠DGB=∠GDB,
∵∠CAB和∠BDC都是弧BC所对的圆周角,
∴∠CAB=∠BDC,
∴∠CAB=∠FGB,
∵∠FGB=∠FBG,
∴∠CAB=∠GBF,
∴AC∥FB.
点评 本题考查的是圆的综合题,涉及到切线的性质,垂径定理,勾股定理,锐角三角函数定义,圆周角定理,平行线的判定,以及等腰三角形的判定,熟练掌握和各种几何图形有关的定理及性质是解本题的关键.


科目:初中数学 来源: 题型:选择题
 如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )| A. | 一直减小 | B. | 先减小后增大 | C. | 一直增大 | D. | 先增大后减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
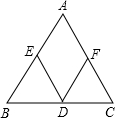 如图,在△ABC中,DE∥AC,DF∥AB.
如图,在△ABC中,DE∥AC,DF∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
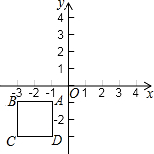 如图,在直角坐标系xOy中,正方形ABCD顶点A(-1,-1)、B(-3,-1).我们规定“把正方形ABCD先沿x轴翻折,再向右平移2个单位”称为一次变换.若正方形ABCD经过2015次这样的变换得到正方形A2015B2015C2015D2015,则点B2015的坐标是(4027,1).
如图,在直角坐标系xOy中,正方形ABCD顶点A(-1,-1)、B(-3,-1).我们规定“把正方形ABCD先沿x轴翻折,再向右平移2个单位”称为一次变换.若正方形ABCD经过2015次这样的变换得到正方形A2015B2015C2015D2015,则点B2015的坐标是(4027,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
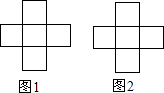 如图,由5个边长为1的正方形组成一个“十”字形,一共有12个顶点,要求:从这12点中取出4个点,直接在图中连出不同大小的正方形,并写出相应的正方形的边长.
如图,由5个边长为1的正方形组成一个“十”字形,一共有12个顶点,要求:从这12点中取出4个点,直接在图中连出不同大小的正方形,并写出相应的正方形的边长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com