练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．用配方法把二次函数y=2x2+3x+1写成y=a（x+m）2+k的形式y=2（x+$\frac{3}{4}$）2-$\frac{1}{8}$．

    分析 把二次函数y=2x2+3x+1用配方法化为顶点式即可．

    解答 解：y=2x2+3x+1
    =2（x+$\frac{3}{4}$）2-$\frac{1}{8}$．
    故答案为：y=2（x+$\frac{3}{4}$）2-$\frac{1}{8}$．

    点评 本题考查的是用配方法把一般式化为顶点式，掌握配方法是解题的关键，y=ax2+bx+c=a（x+$\frac{b}{2a}$）2+$\frac{4ac-{b}^{2}}{4a}$．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．邻居王阿姨在再就业中心的扶持下，创办了“便民”报刊零售点，对经营的某种晚报，王阿姨提供了如下信息：
    ①买进报纸每份0.35元，卖出每份0.5元；
    ②一个月内（以30天计），有22天每天可以卖出250份，其余每天只能卖出150份；
    ③一个月内，每天从报社买进的报纸份数必须相同，当天卖剩下的报纸可以每份0.25元退回报社．
    根据上述信息，请你给王阿姨帮个忙：
    （1）填表：
    一个月内每天买进该晚报（份）150200
    当月利润（元）675800
    （2）设每天从报社买进该晚报x份（150≤x≤250）时，月利润为y元，试求出y关于x的函数关系式，并求月利润的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

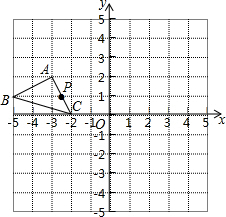    8．如图，在10×10的正方形网格中，每个小正方形的边长均为1个单位．平面直角坐标系和△ABC的位置如图所示．
    （1）画出△ABC关于（-1，-1）的中心对称△A1B1C1；
    （2）P（a，b）是△ABC的边AC上一点，△ABC经平移后点P的对应点为Q（a+6，b+2），请画出上述平移后的△A2B2C2，并写出点A2、C2的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

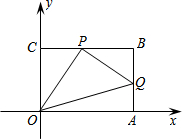    5．已知：如图，在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（6，0）、C（0，4），点P在BC边上运动，过P作PQ⊥OP，交AB边于Q，则AQ的最小值为$\frac{7}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知，线段a，c和∠β（如图），利用直尺和圆规作△ABC，使BC=a，AB=c，∠ABC=∠β（不写作法，保留作图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．分式方程$\frac{3}{x+2}=\frac{5}{x-1}$的解是$-\frac{13}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，我们把杜甫（绝句）整齐排列放在平面直角坐标系中：
    （1）“东”、“窗”和“柳”的坐标依次是：（3，1）、（1，2）和（7，4）；
    （2）将第1行与第3行对调，再将第4列与第6列对调，“里”由开始的坐标（6，1）依次变换到：（6，3）和（4，3）；
    （3）“门”开始的坐标是（1，1），使它的坐标到（3，2），应该哪两行对调，同时哪两列对调？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．在⊙O中，弦AB与弦CD相交于点G，OA⊥CD于点E，过点B作⊙O的切线BF交CD的延长线于点F
    （1）如图1，求证：FG=FB；
    （2）如图2，连接BD、AC，若BD=BG，求证：AC∥BF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图所示，已知∠1=∠2=45°，∠3=100°，求∠4的度数．

    查看答案和解析>>

    同步练习册答案