
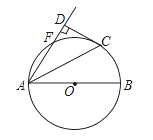
【题目】如图,AB是⊙O的直径,点F、C在⊙O上且![]() , 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
, 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
(1)求证:CD是⊙O的切线;
(2)若![]() , CD=4,求⊙O的半径.
, CD=4,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连结OC,由![]() ,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
(2)连结BC,由AB为直径得∠ACB=90°,由F,C,B三等分半圆得∠BOC=60°,则∠BAC=30°,所以∠DAC=30°,在Rt△ADC中,利用含30度的直角三角形三边的关系得AC=2CD=8,在Rt△ACB中,根据勾股定理求得AB,进而求得⊙O的半径.
(1)证明:连结OC,如图,
∵![]() ,
,
∴∠FAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠FAC=∠OCA,
∴OC∥AF,
∵CD⊥AF,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连结BC,如图,
∵AB为直径,
∴∠ACB=90°,
∵![]() =
=![]() ,
,
∴∠BOC=![]() ×180°=60°,
×180°=60°,
∴∠BAC=30°,
∴∠DAC=30°,
在Rt△ADC中,CD=4,
∴AC=2CD=8,
在Rt△ACB中,BC2+AC2=AB2 ,
即82+(![]() AB)2=AB2 ,
AB)2=AB2 ,
∴AB=![]() ,
,
∴⊙O的半径为![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PMN的面积;③△PAB的周长;④∠APB的大小;⑤直线MN,AB之间的距离.其中会随点P的移动而不改变的是( )

A. ①②③ B. ①②⑤ C. ②③④ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.

(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
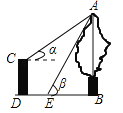
【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①对角线互相垂直且相等的平行四边形是正方形;
②平行四边形、矩形、等边三角形、正方形既是中心对称图形,也是轴对称图形;
③旋转和平移都不改变图形的形状和大小;
④底角是45°的等腰梯形,高是h,则腰长是![]() h;
h;
⑤一组对边平行,另一组对边相等的四边形是平行四边形.
以上正确的命题是( )
A. ①②③④ B. ①②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
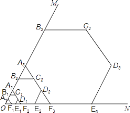
【题目】如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1,边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2, 以A2F2为边作正六边形A2B2C2D2E2F2, 边C2D2所在的直线分别交OM、ON于点A3、F3, 再以A3F3为边作正六边形A3B3C3D3E3F3, …,依此规律,经第4次作图后,点B4到ON的距离是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
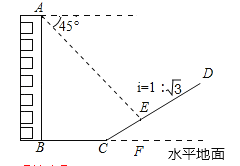
【题目】(8分)如图,一楼房AB后有一假山,其坡度为![]() ,山坡坡面上E点处有一休息亭,测的假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测的假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
查看答案和解析>>
科目:初中数学 来源: 题型:
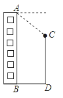
【题目】如图,小明在楼AB顶部的点A处测得楼前一棵树CD的顶端C的俯角为37°,已知楼AB高为18m,楼与树的水平距离BD为8.5m,则树CD的高约为________m(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com