Question

【题目】已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC与点E、F，垂足为O．
（1）如图（1），连接AF、CE．求证四边形AFCE为菱形，并求AF的长；

（2）如图（2），动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周，即点P自A→F→B→A停止，点Q自C→D→E→C停止，在运动过程中，已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．

Answer 1

【答案】
（1）证明：证明：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠EAO=∠FCO，
∵AC的垂直平分线EF，
∴OA=OC，
在△AOE和△COF中，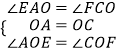
，
∴△AOE≌△COF（ASA），
∴OE=OF，
∵OA=OC，
∴四边形AFCE是平行四边形，
∵EF⊥AC，
∴四边形AFCE是菱形．
∴AF=FC，
设AF=xcm，
则CF=xcm，BF=（8﹣x）cm，
∵四边形ABCD是矩形，
∴∠B=90°，
∴在Rt△ABF中，
由勾股定理得：42+（8﹣x）2=x2 ，
解得x=5，即AF=5cm
（2）解：显然当P点在AF上时，Q点在CD上，此时A、C、P、Q四点不可能构成平行四边形；
同理P点在AB上时，Q点在DE或CE上或P在BF，Q在CD时不构成平行四边形，也不能构成平行四边形．
因此只有当P点在BF上、Q点在ED上时，才能构成平行四边形，
如图所示：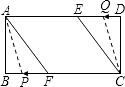

∴以A、C、P、Q四点为顶点的四边形是平行四边形时，PC=QA，
∵点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，
∴PC=5t，QA=12﹣4t，
∴5t=12﹣4t，
解得t= ．
∴以A、C、P、Q四点为顶点的四边形是平行四边形时，t= 秒．
【解析】（1）根据矩形的性质及垂直平分线的性质得出∠EAO=∠FCO，OA=OC，再证明△AOE≌△COF，得出OE=OF，再根据EF⊥AC，可证得四边形AFCE是菱形．由菱形的性质得出AF=CF，然后在Rt△ABF中，设未知数，根据勾股定理建立方程求解即可得出AF的长。
（2）根据已知结合图形，分情况讨论：可知当P点在AF上时，Q点在CD上或P点在AB上时，Q点在DE或CE上或P在BF，Q在CD时，以A、C、P、Q四点为顶点不能构造平行四边形；只有当P点在BF上、Q点在ED上时，才能构成平行四边形，得出PC=QA，建立关于t的方程求解即可。
【考点精析】关于本题考查的勾股定理的概念和平行四边形的性质，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能得出正确答案．