Question

【题目】如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.

（1）当M点在（何处）时，AM＋CM的值最小；
（2）当AM+EM的值最小时，∠BCM=°.
（3）①求证：△AMB≌△ENB；②当M点在何处时，AM＋BM＋CM的值最小，并说明理由.

Answer 1

【答案】
（1）BD的中点
（2）15
（3）解：①∵△ABE是等边三角形，
∴BA=BE，∠ABE=60°，
∵∠MBN=60°，
∴∠MBN-∠ABN=∠ABE-∠ABN，
即∠BMA=∠NBE，
又∵MB=NB，
∴△AMB≌△ENB（SAS）；
②如图，连接CE，

当M点位于BD与CE的交点处时，AM+BM+CM的值最小，
理由如下：连接MN，
由（1）知，△AMB≌△ENB，
∴AM=EN，
∵∠MBN=60°，MB=NB，
∴△BMN是等边三角形，
∴BM=MN，
∴AM+BM+CM=EN+MN+CM，
根据“两点之间线段最短”，得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时，AM+BM+CM的值最小，即等于EC的长.
【解析】（1）①当M点落在BD的中点时，A.M、C三点共线，AM+CM的值最小；
（ 2 ）如图：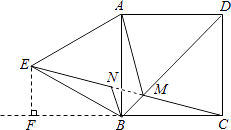

连接CE，当M点位于BD与CE的交点处时，AM+EM的值最小，
过E作EF⊥BC于点F，四边形ABCD是正方形，△ABE是等边三角形，
∴BE=BC，∠EBF=∠ABF-∠ABE=90°-60°=30°，
∴∠BCM= ∠EBF=15°；
（1）根据两点之间线段最短，①当M点落在BD的中点时，A.M、C三点共线，AM+CM的值最小。
（2）连接CE，当M点位于BD与CE的交点处时，AM+EM的值最小，过E作EF⊥BC于点F，根据已知ABCD是正方形，△ABE是等边三角形，得出BE=BC，∠EBF=30°，再根据三角形外角的性质，求出∠BCM的度数即可。
（3）①根据等边三角形的性质得出BA=BE，∠ABE=60°，根据∠MBN=60°，然后证明△AMB≌△ENB即可；②连接CE，当M点位于BD与CE的交点处时，AM+BM+CM的值最小，再根据已知及①的结论证明AM=EN，BM=MN，将AM、BM、CM转化到同一条线段上，根据两点之间线段最短，即可得出答案。