
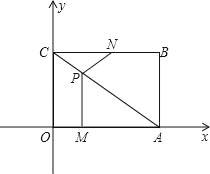
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y��![]() x2+bx+c��x�ύ��A����1��0����B��2��0�����㣬��y�ύ�ڵ�C��
x2+bx+c��x�ύ��A����1��0����B��2��0�����㣬��y�ύ�ڵ�C��

��1����������ߵĽ���ʽ����C�����ꣻ
��2��ֱ��y����x��2����������ڵ��������ڽ��ڵ�D����x�ύ�ڵ�F������AC��CD���߶�AC���߶�DF���ڵ�G����֤����AGF�ա�CGD��
��3��ֱ��y��m��m��0����������ߵĽ���ΪM��N����M�ڵ�N����ࣩ����M����y��ĶԳƵ�Ϊ��M������H������Ϊ��1��0�������ı���NHOM�������Ϊ![]() �����H��OM���ľ���d��
�����H��OM���ľ���d��
���𰸡�(1) y��![]() x2��
x2��![]() x��3,C(0,-3);(2)������;(3)
x��3,C(0,-3);(2)������;(3) ![]()
��������
��1������������y��![]() x2+bx+c��x�ύ��A����1��0����B��2��0�����㣬�ɵ������ߵĽ���ʽ��
x2+bx+c��x�ύ��A����1��0����B��2��0�����㣬�ɵ������ߵĽ���ʽ��
��2������F��-2��0����A��-1��0�����ɵ�AF=1���ٸ��ݵ�D������Ϊ��1��-3������C������Ϊ��0��-3�����ɵ�CD��x�ᣬCD=1���ٸ��ݡ�AFG=��CDG����FAG=��DCG�������ж���AGF�ա�CGD��
��3��������ԳƵ����ʵó�OH=1=M'N�������ж��ı���OM'NH��ƽ���ı��Σ��ٸ����ı���OM'NH�����Ϊ![]() �����OP=
�����OP=![]() ���ٸ��ݵ�M������Ϊ��
���ٸ��ݵ�M������Ϊ��![]() ��
��![]() �����õ�PM'��
�����õ�PM'��![]() Rt��OPM'�У����ù��ɶ����ɵ�OM'=
Rt��OPM'�У����ù��ɶ����ɵ�OM'=![]() ��������OM'��d=
��������OM'��d=![]() �����ɵõ�d=
�����ɵõ�d=![]() ��
��
��1����������y��![]() x2+bx+c��x�ύ��A����1��0����B��2��0�����㣬
x2+bx+c��x�ύ��A����1��0����B��2��0�����㣬
��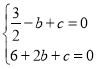 ��
��
���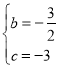 ��
��
��������ߵĽ���ʽy��![]() x2��
x2��![]() x��3��
x��3��
��x��0����y����3��
��C��0����3����
��2��֤������ֱ��EF�Ľ���ʽΪy����x��2��
�൱y��0ʱ��x����2��
��F����2��0����OF��2��
��A����1��0����
��OA��1��
��AF��2��1��1��
��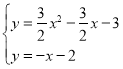 ���
���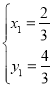 ��
��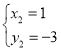 ��
��
�ߵ�D�ڵ������ޣ�
���D��������1����3����
�ߵ�C������Ϊ��0����3����
��CD��x�ᣬCD��1��
���AFG����CDG����FAG����DCG��
����AGF����CGD��
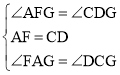
���AGF�ա�CGD��ASA����
��3���������ߵĶԳ���Ϊx����![]() ��
��![]() ��ֱ��y��m��m��0����������ߵĽ���ΪM��N��
��ֱ��y��m��m��0����������ߵĽ���ΪM��N��
���M��N����ֱ��x��![]() �Գƣ�
�Գƣ�
��N��t��m������M��1��t��m����
�ߵ� M����y��ĶԳƵ�Ϊ��M'��
��M'��t��1��m����
���M'��ֱ��y��m�ϣ�
��M'N��x�ᣬ
��M'N��t����t��1����1��
��H��1��0����
��OH��1��M'N��
���ı���OM'NH��ƽ���ı��Σ�
��ֱ��y��m��y�ύ�ڵ�P��
���ı���OM'NH�����Ϊ![]() ��
��
��OH��OP��1��m��![]() ����m��
����m��![]() ��
��
��OP��![]() ��
��
��![]() x2��
x2��![]() x��3��
x��3��![]() ʱ��
ʱ��
���x1����![]() ��x2��
��x2��![]() ��
��
���M����������![]() ��
��![]() ����
����
��M'��![]() ��
��![]() ������PM'��
������PM'��![]() ��
��
��Rt��OPM'��OM'��![]() ��
��![]() ��
��
���ı���OM'NH�����Ϊ ![]() ��
��
��OM'��d��![]() ��
��
��d��![]() ��
��


 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д� �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ij�ֶ�ͯ��ߣ����ÿ������Ϊ40Ԫ���г��������Ź涨���������ÿ�������ܳ���60Ԫ����ÿ����۳�50���������г����鷢�֣����۵���ÿ����2Ԫ��ÿ�������������1���������۵�������![]() Ԫ��ÿ���۳�
Ԫ��ÿ���۳�![]() ����
����
��1�����![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��2����![]() Ϊ����ʱ������ÿ������������߿ɻ�����2250Ԫ��
Ϊ����ʱ������ÿ������������߿ɻ�����2250Ԫ��
��3���賬��ÿ������������߿ɻ���![]() Ԫ����
Ԫ����![]() Ϊ����ʱ
Ϊ����ʱ![]() ������ֵ�Ƕ��٣�
������ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
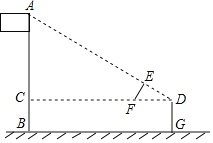
����Ŀ����ͼ��ijУ��ѧ��ȤС���������Ƶ�ֱ��������Ӳֽ��DEF�������ٳ����AB�ĸ߶ȣ�����ͨ����������λ�ã�ʹб��DF����汣��ƽ�У���ʹ��DE����˶���A��ͬһֱ���ϣ���֪DE��1�ף�EF��0.5�ף����D������ľ���DG��3�ף�����˵�ˮƽ����DC��40�ף�����˵ĸ߶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
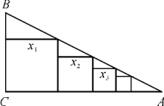
����Ŀ����ͼ��ʾ����Rt��ABC�У���C=90����BC=1��AC=4���ѱ߳��ֱ�Ϊ![]() ��
��![]() ��
��![]() ������
������![]() ��n
��n![]() �����������η�����ABC�У����n�������εı߳�
�����������η�����ABC�У����n�������εı߳�![]() _______________���ú�n��ʽ�ӱ�ʾ����
_______________���ú�n��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��ͼ����ͼ��ʾ�����½��ۣ���abc��0����4ac��b2����2a+b��0�����䶥������Ϊ��
��ͼ����ͼ��ʾ�����½��ۣ���abc��0����4ac��b2����2a+b��0�����䶥������Ϊ��![]() ����2�����ݵ�x��
����2�����ݵ�x��![]() ʱ��y��x���������С����a+b+c��0��ȷ���У�������
ʱ��y��x���������С����a+b+c��0��ȷ���У�������

A. 3�� B. 4�� C. 5�� D. 6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У��ı���OABCΪ���Σ���A��B������ֱ�Ϊ��4��0������4��3��������M��N�ֱ��O��Bͬʱ��������ÿ��1����λ���ٶ��˶������У���M��OA���յ�A�˶�����N��BC���յ�C�˶�������M��MP��OA����AC��P������NP����֪�����˶���x�룮
��1����P������꣨�ú�x�Ĵ���ʽ��ʾ����
��2��������NPC���S�ı���ʽ����������S�����ֵ����Ӧ��xֵ��
��3�����ı���OMPC�����ΪS1���ı���ABNP�����ΪS2�������x��ȡֵ��Χ����S1��S2�Ĵ�С��ϵ��˵�����ɣ�
��4����xΪ��ֵʱ����NPC��һ�����������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]()
(1)д������ͼ��Ŀ��ڷ���������ͶԳ���.
(2)�жϵ�![]() �Ƿ��ڸú���ͼ���ϣ���˵������.
�Ƿ��ڸú���ͼ���ϣ���˵������.
(3)����Ը�����������������Ľ���Ϊ����������ε����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
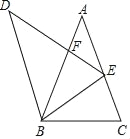
����Ŀ����ͼ������ABC�У���A=36�㣬AC=AB=2������ABC�Ƶ�B��ʱ�뷽����ת�õ���DBE��ʹ��E�ڱ�AC�ϣ�DE��AB�ڵ�F������AFE����DBF�����֮�ȵ��ڣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ʡ���ϣ�ijˮ����ֳ������ˮ��İ��̣������㹻����Ϊһ�ߣ����ܳ�Ϊ80m��Χ����ˮ����Χ������ͼ��ʾ���٢ڢ���������������������������������ȣ���BC�ij���Ϊxm����������ABCD�����Ϊym2��
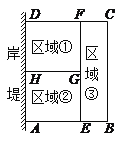
��1����AE�ij�����x�Ĵ���ʽ��ʾ��
��2����y=108m2ʱ����x��ֵ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com