
【题目】探究证明:
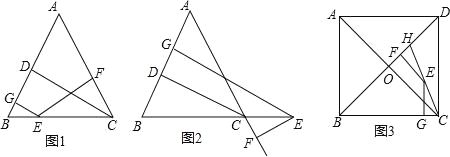
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
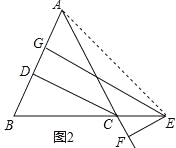
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
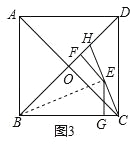
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .
【答案】(1)证明见解析
(2)CD=EG﹣EF,
(3)5![]() .
.

【解析】
试题分析:(1)根据S△ABC=S△ABE+S△ACE,得到![]() ABCD=
ABCD=![]() ABEG+
ABEG+![]() ACEF,根据等式的性质即可得到结论;
ACEF,根据等式的性质即可得到结论;
(2)由于S△ABC=S△ABE﹣S△ACE,于是得到![]() ABCD=
ABCD=![]() ABEG﹣
ABEG﹣![]() ACEF,根据等式的性质即可得到结论;
ACEF,根据等式的性质即可得到结论;
(3)根据正方形的性质得到AB=BC=10,∠ABC=90°,AC⊥BD,根据勾股定理得到AC=10![]() ,由于S△BCH=S△BCE+S△BHE,得到
,由于S△BCH=S△BCE+S△BHE,得到![]() BHOC=
BHOC=![]() BCEG+
BCEG+![]() BHEF,根据等式的性质即可得到结论.
BHEF,根据等式的性质即可得到结论.
试题解析:(1)如图1,连接AE,
∵EG⊥AB,EF⊥AC,CD⊥AB,
∵S△ABC=S△ABE+S△ACE,
∴![]() ABCD=
ABCD=![]() ABEG+
ABEG+![]() ACEF,
ACEF,
∵AB=AC,
∴CD=EG+EF;
(2)CD=EG﹣EF,
理由:连接AE,
∵EG⊥AB,EF⊥AC,CD⊥AB,
∵S△ABC=S△ABE﹣S△ACE,
∴![]() ABCD=
ABCD=![]() ABEG﹣
ABEG﹣![]() ACEF,
ACEF,
∵AB=AC,
∴CD=EG﹣EF;
故答案为:CD=EG﹣EF;
(3)∵四边形ABCD是正方形,
∴AB=BC=10,∠ABC=90°,AC⊥BD,
∴AC=10![]() ,
,
∴OC=![]() AC=5
AC=5![]() ,
,
连接BE.
∵EF⊥BD于点F,EG⊥BC于点G,
∵S△BCH=S△BCE+S△BHE,
∴![]() BHOC=
BHOC=![]() BCEG+
BCEG+![]() BHEF,
BHEF,
∴OC=EG+EF=5![]() ,
,
故答案为:5![]() .
.





科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。
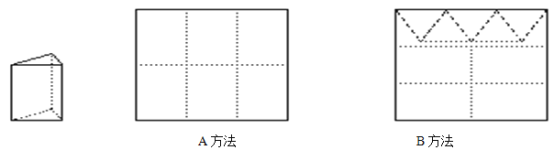
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)
【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
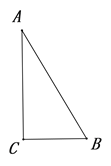
已知:如图,在![]() △
△![]() 中,
中, ![]() °,
°,![]() °.
°.
求证: ![]() .
.
证明:
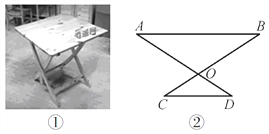
【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得![]() ,
, ![]() ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度![]() .
.
求:桌面与地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列方程的特征及其解的特点.
①x+![]() =-3的解为x1=-1,x2=-2;
=-3的解为x1=-1,x2=-2;
②x+![]() =-5的解为x1=-2,x2=-3;
=-5的解为x1=-2,x2=-3;
③x+![]() =-7的解为x1=-3,x2=-4.
=-7的解为x1=-3,x2=-4.
解答下列问题:
(1)请你写出一个符合上述特征的方程为____________,其解为x1=-4,x2=-5;
(2)根据这类方程特征,写出第n个方程为________________,其解为x1=-n,x2=-n-1;
(3)请利用(2)的结论,求关于x的方程x+![]() =-2(n+2)(其中n为正整数)的解.
=-2(n+2)(其中n为正整数)的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )
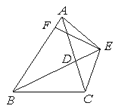
A.①②③ B.①③④ C.①②④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为贯彻政府报告中“大众创业、万众创新”的精神,某镇对辖区内所有的小微企业按年利润w(万元)的多少分为以下四个类型:A类(w<10),B类(10≤w<20),C类(20≤w<30),D类(w≥30),该镇政府对辖区内所有小微企业的相关信息进行统计后,绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题:

(1)该镇本次统计的小微企业总个数是 ,扇形统计图中B类所对应扇形圆心角的度数为 度,请补全条形统计图;
(2)为了进一步解决小微企业在发展中的问题,该镇政府准备召开一次座谈会,每个企业派一名代表参会.计划从D类企业的4个参会代表中随机抽取2个发言,D类企业的4个参会代表中有2个来自高新区,另2个来自开发区.请用列表或画树状图的方法求出所抽取的2个发言代表都来自高新区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°, AD平分∠BAC交BC于D,DE⊥AB于E
求证:(1)△ACD≌△AED;(2)若AB=6,求△DEB的周长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.

原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据___________,SAS
易证△AFG≌___________△AEF
,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°.点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系______________∠B+∠D=180°
时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com