
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
【答案】(1)9,9;(2)![]() ;(3)推荐甲参加比赛合适.
;(3)推荐甲参加比赛合适.
【解析】
试题分析:(1)根据中位数的定义先把这组数据从小到大排列,再找出最中间两个数的平均数即可求出①;根据平均数的计算公式即可求出②;
(2)根据方差的计算公式S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2]代值计算即可;
)2]代值计算即可;
(3)根据方差的意义:反映了一组数据的波动大小,方差越大,波动性越大,反之也成立,即可得出答案.
解:(1)甲的中位数是:![]() =9;
=9;
乙的平均数是:(10+7+10+10+9+8)÷6=9;
故答案为:9,9;
(2)S甲2=![]() [(10﹣9)2+(8﹣9)2+(9﹣9)2+(8﹣9)2+(10﹣9)2+(9﹣9)2]=
[(10﹣9)2+(8﹣9)2+(9﹣9)2+(8﹣9)2+(10﹣9)2+(9﹣9)2]=![]() ;
;
(3)∵![]() =
=![]() ,S甲2<S乙2,
,S甲2<S乙2,
∴推荐甲参加比赛合适.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】对于0,1以及真分数p,q,r,若p<q<r,我们称q为p和r的中间分数.为了帮助我们找中间分数,制作了下表:

两个不等的正分数有无数多个中间分数.例如:上表中第③行中的3个分数![]() 、
、![]() 、
、![]() ,有
,有![]() ,所以
,所以![]() 为
为![]() 和
和![]() 的一个中间分数,在表中还可以找到
的一个中间分数,在表中还可以找到![]() 和
和![]() 的中间分数
的中间分数![]() ,
, ![]() ,
, ![]() ,
, ![]() .把这个表一直写下去,可以找到
.把这个表一直写下去,可以找到![]() 和
和![]() 更多的中间分数.
更多的中间分数.
(1)按上表的排列规律,完成下面的填空:
①上表中括号内应填的数为 ;
②如果把上面的表一直写下去,那么表中第一个出现的![]() 和
和![]() 的中间分数是 ;
的中间分数是 ;
(2)写出分数![]() 和
和![]() (a、b、c、d均为正整数,
(a、b、c、d均为正整数, ![]() ,
, ![]() )的一个中间分数(用含a、b、c、d的式子表示),并证明;
)的一个中间分数(用含a、b、c、d的式子表示),并证明;
(3)若![]() 与
与![]() (m、n、s、 t均为正整数)都是
(m、n、s、 t均为正整数)都是![]() 和
和![]() 的中间分数,则
的中间分数,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,(1)已知∠ABC,射线ED∥AB,过点E作∠DEF=∠ABC,试说明BC∥EF;
(2)如图②,已知∠ABC,射线ED∥AB,∠ABC+∠DEF=180°.判断直线BC与直线EF的位置关系,并说明理由;
(3)根据以上探究,你发现了一个什么结论?请你写出来;
(4)如图③,已知AC⊥BC,CD⊥AB,DE⊥AC,HF⊥AB,若∠1=48°,试求∠2的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究证明:
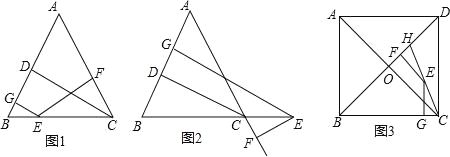
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表所示为装运、销售甲、乙、丙三种蔬菜的重量及利润。某公司计划用20辆汽车装运甲、乙、丙三种蔬菜共36吨到某地销售.规定每辆汽车满载,每车只装一种蔬菜,每种蔬菜不少于一车。应如何安排,可使公司获得利润18300元?
甲 | 乙 | 丙 | |
每辆汽车装运的吨数 | 2 | 1 | 1.5 |
每吨蔬菜可获利润(百元) | 5 | 7 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)若D(x,0)是x轴上原点左侧的一点,且满足kx+b-![]() <0,求x的取值范围.
<0,求x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定个人发表文章、出版图书获得稿费的纳税计算方法是:(l)稿费不高于800元的不纳税;(2)稿费高于800元又不高于4000元的,减除其中的800元,其余部分按20%纳税:(3)稿费高于4000元,减除稿酬的20%,其余部分按20%纳税.今知丁老师获得一笔稿费,并缴纳个人所得税600元,问:丁老师的这笔稿费有多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0(a≠0)的求根公式时,对于b2﹣4ac>0的情况,她是这样做的:
由于a≠0,方程ax2+bx+c=0变形为:
x2+![]() x=﹣
x=﹣![]() ,…第一步
,…第一步
x2+![]() x+(
x+(![]() )2=﹣
)2=﹣![]() +(
+(![]() )2,…第二步
)2,…第二步
(x+![]() )2=
)2=![]() ,…第三步
,…第三步
x+![]() =
=![]() (b2﹣4ac>0),…第四步
(b2﹣4ac>0),…第四步
x=![]() ,…第五步
,…第五步
嘉淇的解法从第 步开始出现错误;事实上,当b2﹣4ac>0时,方程ax2+bx+c=0(a≠O)的求根公式是 .
用配方法解方程:x2﹣2x﹣24=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com