
����Ŀ������0��1�Լ������p��q��r����p<q<r�����dz�qΪp��r���м������Ϊ�˰����������м�������������±���

�������ȵ�����������������м���������磺�ϱ��е������е�3������![]() ��
��![]() ��
��![]() ����
����![]() ������
������![]() Ϊ
Ϊ![]() ��
��![]() ��һ���м�������ڱ��л������ҵ�
��һ���м�������ڱ��л������ҵ�![]() ��
��![]() ������
������![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ���������һֱд��ȥ�������ҵ�
���������һֱд��ȥ�������ҵ�![]() ��
��![]() �����������
�����������
��1�����ϱ������й��ɣ�����������գ�
���ϱ���������Ӧ�����Ϊ ��
�����������ı�һֱд��ȥ����ô���е�һ�����ֵ�![]() ��
��![]() �������� ��
�������� ��
��2�������![]() ��
��![]() ��a��b��c��d����������
��a��b��c��d���������� ![]() ��
�� ![]() ����һ���м�������ú�a��b��c��d��ʽ�ӱ�ʾ������֤����
����һ���м�������ú�a��b��c��d��ʽ�ӱ�ʾ������֤����
��3����![]() ��
��![]() ��m��n��s�� t��������������
��m��n��s�� t��������������![]() ��
��![]() ����������
���м��������![]() ����СֵΪ ��
����СֵΪ ��
���𰸡���1����![]() ����
����![]() ��2��֤����������3��1504
��2��֤����������3��1504
�������������������1���ٹ۲�ÿһ�еĹ��ɿɵ�����λ�ڵڢ��У��������еĹ��ɿ�֪��![]() ��
��
�ڹ۲�����֪��һ�����ֵ�![]() ��
��![]() ���м�����ڵڢ��У���
���м�����ڵڢ��У���![]() ��
��
��2���𰸲�Ψһ�����ݱ����й۲쵽�ģ�����Ϊ![]() ��ͨ���Ƶ�֤�����ɵã�
��ͨ���Ƶ�֤�����ɵã�
��3���������п�֪![]() ��
��![]() ��������
��������![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �ȣ��ɴ˿ɵ�.
�ȣ��ɴ˿ɵ�.
�����������1���ٹ۲�ÿһ�еĹ��ɿɵ�����λ�ڵڢ��У������ӵ������֪��![]() ��
��
�ڹ۲�����֪��һ�����ֵ�![]() ��
��![]() ���м�����ڵڢ��У���
���м�����ڵڢ��У���![]() ��
��
�ʴ�Ϊ����![]() ����
����![]() ��
��
��2��������۲�Ψһ��֤����Ψһ���磺
���ۣ� ![]() ��
��
��a��b��c��d���������� ![]() ��
�� ![]() ��
��
��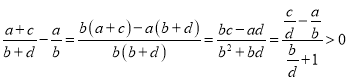 ��
��
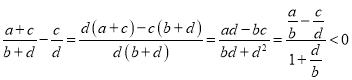 ��
��
��![]() ��
��
��3���������п�֪![]() ��
��![]() ��������
��������![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �ȣ��ɴ˿ɵ�mn����СֵΪ1504��
�ȣ��ɴ˿ɵ�mn����СֵΪ1504��
�ʴ�Ϊ��1504.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
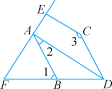
����Ŀ����ͼ����֪��1=��BDC����2+��3=180�㣮
��1�������ж�DA��CE��λ�ù�ϵ����˵�����ɣ�
��2����DAƽ����BDC��CE��AE��E����1=70�㣬������FAB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㹻��ij����κ������ο�Ƭ����ͼ��

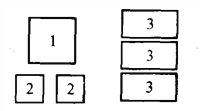
��1����ͼ�����ѡȡ1�š�2�š�3�ſ�Ƭ�ֱ�Ϊ1�š�2�š�3�ţ���ƴ��һ��������(���ص���϶)���뻭����������εIJ�ͼ��������ƴͼǰ�����֮��Ĺ�ϵ˵����������εĴ������壮
��������εĴ���������______________��
��2��С���������Ʒ������Ͷ���ʽ�˷�![]() ��
��
��ô����2�ſ�Ƭ_________�ţ�3�ſ�Ƭ_____________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����C����O��һ�㣬OD��BC�ڵ�D������C����O�����ߣ���OD���ӳ����ڵ�E������BE��
��1����֤��BE����O���У�
��2����OE����O�ڵ�F����DF=1��BC=2![]() ������Ӱ���ֵ������
������Ӱ���ֵ������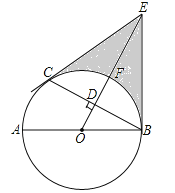
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ӳֽ�������������ӣ�ÿ��������3�����β����2���������ε�����ɣ�Ӳֽ����ͼ���ַ����ü����ü���߽��ϲ������ã�
A��������6�����棻 B��������4�������5�����档
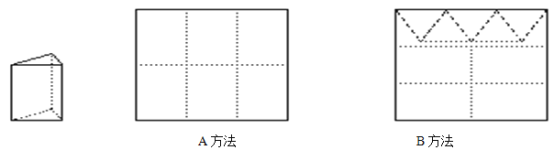
����38��Ӳֽ�壬�ü�ʱx����A������������B������
��1����x�Ĵ���ʽ�ֱ��ʾ�ü����IJ���͵���ĸ�����
��2�����ü����IJ���͵���ǡ��ȫ�����꣬���������ٸ����ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
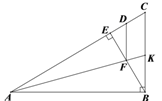
����Ŀ����ͼ������ABC������ABC=90����BE��AC�ڵ�E����D��AC������AD��AB��AKƽ�֡�CAB�����߶�BE�ڵ�F������CB�ڵ�K��
��1����ͼ���ҳ�һ��ȫ�������Σ���֤����
��2����֤��FD��BC ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AO��BO��CO��DO�ֱ����ı���ABCD���ĸ��ڽǵ�ƽ���ߡ�
��1���жϡ�AOB���COD��������������ϵ��Ϊʲô��
��2������AOD=��BOC��AB��CD��������λ�ù�ϵ��Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ABC�͡�ACB��ƽ����BE��CF�ཻ�ڵ�P��
��1������ABC=70�㣬��ACB=50�㣬���BPC=�� ���㣻
��2����֤����BPC=180�㩁![]() ����ABC+��ACB����
����ABC+��ACB����
��3������A=�������BPC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ϊ�Ӽס��������˶�Ա��ѡ��һ�˲μӱ����������ǽ��������β��ԣ����Գɼ����±�����λ��������
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | ƽ���ɼ� | ��λ�� | |
�� | 10 | 8 | 9 | 8 | 10 | 9 | 9 | �� |
�� | 10 | 7 | 10 | 10 | 9 | 8 | �� | 9.5 |
��1����ɱ�����բ� ���� ��
��2�����������β��Գɼ��ķ��
��3���������β��Գɼ�����Ϊ![]() ������Ϊ�Ƽ�˭�μӱ��������ʣ���˵�����ɣ�
������Ϊ�Ƽ�˭�μӱ��������ʣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com