
【题目】如图,AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线。
(1)判断∠AOB与∠COD有怎样的数量关系,为什么?
(2)若∠AOD=∠BOC,AB、CD有怎样的位置关系,为什么?

【答案】(1)∠AOB+∠COD=180°,理由见解析;(2)AB∥CD,理由见解析
【解析】试题分析:(1)本题考查的是角平分线的性质;(2)本题利用角平分线的性质和平行线的判定解决即可.
试题解析:
(1)∠AOB+∠COD=180°
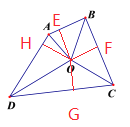
因为:过点O分别作OE⊥AB,OF⊥BC,OG⊥CD,OH⊥AD,∵AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线,∴OE=OF=OG=OH,∴∠AOH=∠AOE, ∠BOF=∠BOE, ∠COF=∠COG, ∠DOG=∠HOD,∴∠AOE+∠BOE+∠COG+∠DOG=∠AOH+∠BOF+ ∠COF+∠HOD,∴∠AOB+∠COD=180°;
(2)AB∥CD.
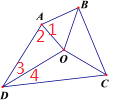
由(1)知∠AOB+∠COD=180°,∴∠COB+∠AOD=180°,∵∠AOD=∠BOC,∴∠AOD=90°,∴∠2+∠3=90°,∵∠1=∠2,∠3=∠4,∴∠1+∠2+∠3+∠4=180°,∴AB∥CD.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数![]() 的图象有一个交点为A(m,2).
的图象有一个交点为A(m,2).
(1)求m的值及正比例函数y=kx的表达式;
(2)试判断点B(2,3)是否在正比例函数图象上,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次物理竞赛中,有一道四选二的双项选择题,评分标准是:多选或只要选错一项就不得分,只选一项且对得1分,全对得3分.
(1)小娟在不会做的情况下,根据题意决定任选一项作为答案,求她得到1分的概率.
(2)小娜在不会做的情况下,根据题意决定任选两项作答案,用列表法表示小娜答案的所有可能结果,并求她得到3分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于0,1以及真分数p,q,r,若p<q<r,我们称q为p和r的中间分数.为了帮助我们找中间分数,制作了下表:

两个不等的正分数有无数多个中间分数.例如:上表中第③行中的3个分数![]() 、
、![]() 、
、![]() ,有
,有![]() ,所以
,所以![]() 为
为![]() 和
和![]() 的一个中间分数,在表中还可以找到
的一个中间分数,在表中还可以找到![]() 和
和![]() 的中间分数
的中间分数![]() ,
, ![]() ,
, ![]() ,
, ![]() .把这个表一直写下去,可以找到
.把这个表一直写下去,可以找到![]() 和
和![]() 更多的中间分数.
更多的中间分数.
(1)按上表的排列规律,完成下面的填空:
①上表中括号内应填的数为 ;
②如果把上面的表一直写下去,那么表中第一个出现的![]() 和
和![]() 的中间分数是 ;
的中间分数是 ;
(2)写出分数![]() 和
和![]() (a、b、c、d均为正整数,
(a、b、c、d均为正整数, ![]() ,
, ![]() )的一个中间分数(用含a、b、c、d的式子表示),并证明;
)的一个中间分数(用含a、b、c、d的式子表示),并证明;
(3)若![]() 与
与![]() (m、n、s、 t均为正整数)都是
(m、n、s、 t均为正整数)都是![]() 和
和![]() 的中间分数,则
的中间分数,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
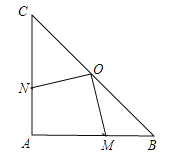
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM .
(1)证明:OM = ON;
(2)四边形AMON面积是否发生变化,若发生变化说明理由;若不变,请你求出四边形AMON的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
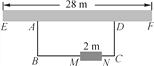
【题目】如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).现有砌60米长的墙的材料.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成480平方米的矩形花园,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
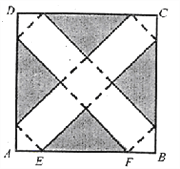
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于底面上一点).已知E、F在AB边上,是被剪去一个等腰直角三角形斜边的两个端点,设AE=BF=xcm.
(1)若折成的包装盒恰好是正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)若D(x,0)是x轴上原点左侧的一点,且满足kx+b-![]() <0,求x的取值范围.
<0,求x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com