
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM .
(1)证明:OM = ON;
(2)四边形AMON面积是否发生变化,若发生变化说明理由;若不变,请你求出四边形AMON的面积.
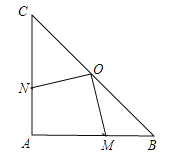
【答案】(1)见解析 (2)4cm2
【解析】试题分析:
(1) 分析条件可知,要证明OM=ON需要利用全等三角形进行. 易知△ABC是等腰直角三角形,根据“O是BC的中点”这一条件容易联想到利用等腰三角形“三线合一”的性质来构造全等三角形. 连接OA后容易发现△OAN与△OBM全等,进而得到OM=ON.
(2) 借助第(1)小题的辅助线作法可知,AO将四边形AMON分割为△OAN与△OAM. 由第(1)小题的证明可知,△OAN的面积等于△OBM的面积. 利用这一关系,实际上将四边形AMON的面积转化为了△OAB的面积. 因为△OAB的面积不受动点运动的影响,所以四边形AMON的面积不变. 根据等腰三角形的性质容易求得△OAB的面积,即得四边形AMON的面积.
试题解析:
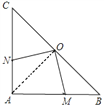
(1) 连接OA. (如图)
∵在Rt△ABC中,AB=AC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,即∠ABO=45°,
∵O是BC的中点,且△ABC是等腰直角三角形,
∴AO⊥BC,
∴在Rt△AOB中,∠OAB=90°-∠ABO=90°-45°=45°,
∴∠OAB=∠ABO,
∴OA=OB,
∵O是BC的中点,且△ABC是等腰直角三角形,
又∵∠BAC=90°,
∴![]() ,
,
∴∠OAC=∠ABO=45°,即∠OAN=∠OBM,
∵在△OAN与△OBM中:
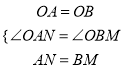 ,
,
∴△OAN≌△OBM (SAS),
∴ON=OM,即OM=ON.
(2) 在动点运动过程中,四边形AMON面积不变.
下面求解四边形AMON的面积.
连接OA.
由第(1)小题的证明可知:△OAN≌△OBM,
∴△OAN的面积等于△OBM的面积,
∵四边形AMON的面积等于△OAN的面积与△OAM的面积之和,
∴四边形AMON的面积等于△OBM的面积与△OAM的面积之和,
∵△OBM的面积与△OAM的面积之和等于△OAB的面积,
∴四边形AMON的面积等于△OAB的面积,
∵O是BC的中点,且△ABC是等腰直角三角形,
∴△OAB的面积等于△ABC的面积的一半,
∵AB=AC=4cm,
∴Rt△ABC的面积为: ![]() (cm2),
(cm2),
∴△OAB的面积为: ![]() (cm2),
(cm2),
∴四边形AMON的面积为:4cm2.


科目:初中数学 来源: 题型:
【题目】某市今年中考理、化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试.小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(1)用“列表法”或“树状图法”表示所有可能出现的结果;
(2)小刚抽到物理实验B和化学实验F(记作事件M)的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
小明遇到这样一个问题:求计算![]() 所得多项式的一次项系数.
所得多项式的一次项系数.
小明想通过计算![]() 所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
他决定从简单情况开始,先找![]() 所得多项式中的一次项系数.通过观察发现:
所得多项式中的一次项系数.通过观察发现:

也就是说,只需用![]() 中的一次项系数1乘以
中的一次项系数1乘以![]() 中的常数项3,再用
中的常数项3,再用![]() 中的常数项2乘以
中的常数项2乘以![]() 中的一次项系数2,两个积相加
中的一次项系数2,两个积相加![]() ,即可得到一次项系数.
,即可得到一次项系数.
延续上面的方法,求计算![]() 所得多项式的一次项系数.可以先用
所得多项式的一次项系数.可以先用![]() 的一次项系数1,
的一次项系数1, ![]() 的常数项3,
的常数项3, ![]() 的常数项4,相乘得到12;再用
的常数项4,相乘得到12;再用![]() 的一次项系数2,
的一次项系数2, ![]() 的常数项2,
的常数项2, ![]() 的常数项4,相乘得到16;然后用
的常数项4,相乘得到16;然后用![]() 的一次项系数3,
的一次项系数3, ![]() 的常数项2,
的常数项2, ![]() 的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
参考小明思考问题的方法,解决下列问题:
(1)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(2)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(3)若计算![]() 所得多项式的一次项系数为0,则
所得多项式的一次项系数为0,则![]() =_________.
=_________.
(4)若![]() 是
是![]() 的一个因式,则
的一个因式,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。
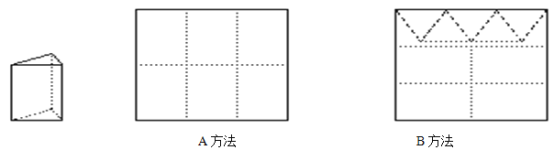
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“春种一粒栗,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物。我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续多年全国第一.2016年全国谷子的种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg.请解答下列问题:
(1)求我省2016年谷子的种植面积是多少万亩;
(2)2017年,若我省谷子的平均亩产量仍保持160kg不变,要使我省谷子的年总产量达到52万吨,那么今年我省应再多种植多少万亩的谷子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线。
(1)判断∠AOB与∠COD有怎样的数量关系,为什么?
(2)若∠AOD=∠BOC,AB、CD有怎样的位置关系,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
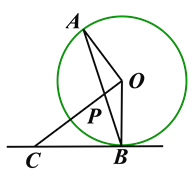
【题目】如图,AB是⊙O的弦,点C是在过点B的切线上,且OC⊥OA,OC交AB于点P.
(1)判断△CBP的形状,并说明理由;
(2)若⊙O的半径为6,AP=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)
【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
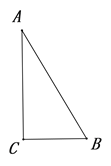
已知:如图,在![]() △
△![]() 中,
中, ![]() °,
°,![]() °.
°.
求证: ![]() .
.
证明:
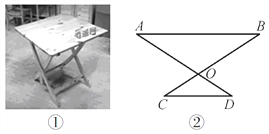
【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得![]() ,
, ![]() ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度![]() .
.
求:桌面与地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为贯彻政府报告中“大众创业、万众创新”的精神,某镇对辖区内所有的小微企业按年利润w(万元)的多少分为以下四个类型:A类(w<10),B类(10≤w<20),C类(20≤w<30),D类(w≥30),该镇政府对辖区内所有小微企业的相关信息进行统计后,绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题:

(1)该镇本次统计的小微企业总个数是 ,扇形统计图中B类所对应扇形圆心角的度数为 度,请补全条形统计图;
(2)为了进一步解决小微企业在发展中的问题,该镇政府准备召开一次座谈会,每个企业派一名代表参会.计划从D类企业的4个参会代表中随机抽取2个发言,D类企业的4个参会代表中有2个来自高新区,另2个来自开发区.请用列表或画树状图的方法求出所抽取的2个发言代表都来自高新区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com