
【题目】如图,在△ABC中,∠C=90°, AD平分∠BAC交BC于D,DE⊥AB于E
求证:(1)△ACD≌△AED;(2)若AB=6,求△DEB的周长。

【答案】(1)证明见解析;(2)6
【解析】试题分析:(1)根据角平分线性质求出CD=DE,根据HL定理求出两三角形全等即可;
(2)根据全等三角形的性质得到AC=AE,CD=DE,由于AC=BC,等量代换得到BC=AE,于是得到△DEB的周长=DB+DE+EB=DB+CD+EB=CB+BE=AE+BE=6.
试题解析:(1)∵AD平分∠CAB,DE⊥AB,∠C=90,
∴CD=ED,∠DEA=∠C=90,
在Rt△ACD和Rt△AED中,
![]() ,
,
∴Rt△ACD≌Rt△AED(HL);
(2)∵△ACD≌△AED,
∴AC=AE,CD=DE,
∵AC=BC,
∴BC=AE,
∴△DEB的周长=DB+DE+EB=DB+CD+EB=CB+BE=AE+BE=AB=6.


科目:初中数学 来源: 题型:
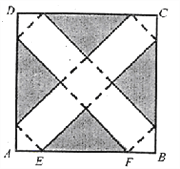
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于底面上一点).已知E、F在AB边上,是被剪去一个等腰直角三角形斜边的两个端点,设AE=BF=xcm.
(1)若折成的包装盒恰好是正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
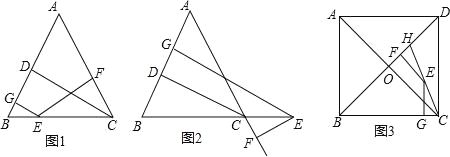
【题目】探究证明:
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)若D(x,0)是x轴上原点左侧的一点,且满足kx+b-![]() <0,求x的取值范围.
<0,求x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
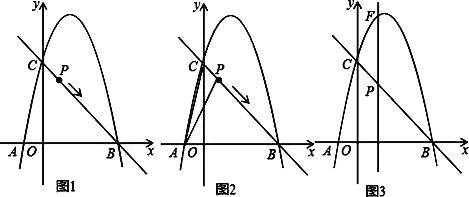
【题目】如图1,抛物线y=ax2+bx+5的图象过A(﹣1,0),B(5,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒![]() 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
(1)求抛物线的表达式;
(2)如图2,当t=1时,若点Q是X轴上的一个动点,如果以Q,P,B为顶点的三角形与△ABC相似,求出Q点的坐标;
(3)如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.
①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接BF,将△PBF沿BF折叠得到△P′BF,当t为何值时,四边形PFP′B是菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定个人发表文章、出版图书获得稿费的纳税计算方法是:(l)稿费不高于800元的不纳税;(2)稿费高于800元又不高于4000元的,减除其中的800元,其余部分按20%纳税:(3)稿费高于4000元,减除稿酬的20%,其余部分按20%纳税.今知丁老师获得一笔稿费,并缴纳个人所得税600元,问:丁老师的这笔稿费有多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=![]() ,AF=
,AF=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图像经过点(-1.-5),且与正比例函数y=![]() x的图象相交于点(2,m).
x的图象相交于点(2,m).
(1)求m的值;
(2)求一次函数y=kx+b的解析式;
(3)求这两个函数图像与x轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
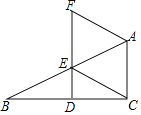
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com