
【题目】观察下列方程的特征及其解的特点.
①x+![]() =-3的解为x1=-1,x2=-2;
=-3的解为x1=-1,x2=-2;
②x+![]() =-5的解为x1=-2,x2=-3;
=-5的解为x1=-2,x2=-3;
③x+![]() =-7的解为x1=-3,x2=-4.
=-7的解为x1=-3,x2=-4.
解答下列问题:
(1)请你写出一个符合上述特征的方程为____________,其解为x1=-4,x2=-5;
(2)根据这类方程特征,写出第n个方程为________________,其解为x1=-n,x2=-n-1;
(3)请利用(2)的结论,求关于x的方程x+![]() =-2(n+2)(其中n为正整数)的解.
=-2(n+2)(其中n为正整数)的解.
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】一次物理竞赛中,有一道四选二的双项选择题,评分标准是:多选或只要选错一项就不得分,只选一项且对得1分,全对得3分.
(1)小娟在不会做的情况下,根据题意决定任选一项作为答案,求她得到1分的概率.
(2)小娜在不会做的情况下,根据题意决定任选两项作答案,用列表法表示小娜答案的所有可能结果,并求她得到3分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
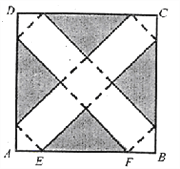
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于底面上一点).已知E、F在AB边上,是被剪去一个等腰直角三角形斜边的两个端点,设AE=BF=xcm.
(1)若折成的包装盒恰好是正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图ΔABC中,∠B =∠C,BD=CF,BE=CD,∠EDF=α,则下列结论正确的是( )

A. 2α+∠A=90° B. 2α+∠A=180°
C. α+∠A=90° D. α+∠A=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,(1)已知∠ABC,射线ED∥AB,过点E作∠DEF=∠ABC,试说明BC∥EF;
(2)如图②,已知∠ABC,射线ED∥AB,∠ABC+∠DEF=180°.判断直线BC与直线EF的位置关系,并说明理由;
(3)根据以上探究,你发现了一个什么结论?请你写出来;
(4)如图③,已知AC⊥BC,CD⊥AB,DE⊥AC,HF⊥AB,若∠1=48°,试求∠2的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究证明:
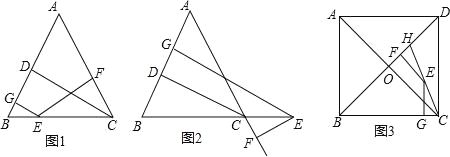
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)若D(x,0)是x轴上原点左侧的一点,且满足kx+b-![]() <0,求x的取值范围.
<0,求x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图像经过点(-1.-5),且与正比例函数y=![]() x的图象相交于点(2,m).
x的图象相交于点(2,m).
(1)求m的值;
(2)求一次函数y=kx+b的解析式;
(3)求这两个函数图像与x轴所围成的三角形面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com