

分析 (1)根据两点间的距离公式,可得答案;
(2)根据两点间的距离公式,点在线段上,可得最小值;
(3)根据两点间的距离公式,点在线段上,可得答案.
解答 解:(1)根据题意,得|x+2|+|x-1|,故答案为:|x+2|+|x-1|;
(2)①根据数轴可得-2、4,故答案为:-2,4;
②4;不小于0且不大于2,2;
故答案为:4;不小于0且不大于2,2;
(3)|x-3|+|x-2|+|x|+|x+1|=(|x-3|+|x+1|)+(|x-2|+|x|)
要使|x-3|+|x+1|的值最小,x的值取-1到3之间(包括-1、3)的任意一个数,要使|x-2|+|x1|的值最小,x取0到2之间(包括0、2)的任意一个数,显然当x取0到2之间(包括0、2)的任意一个数能同时满足要求,不妨取x=0代入原式,得|x-3|+|x-2|+|x|+|x+1|=3+2+0+1=6
方法二:当x取在0到2之间(包括0、2)时,
|x-3|+|x-2|+|x|+|x+1|
=-(x-3)-(x-2)+x+(x+1)
=-x+3-x+2+x+x+1
=6.
点评 本题考查了绝对值,读懂题目信息,理解绝对值的几何意义是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 正方形的对角线互相平分且垂直 | |
| C. | 菱形的对角线相等且互相垂直 | |
| D. | 对角线互相平分且相等的四边形是矩形 | |
| E. | 对角线互相平分且相等的四边形是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
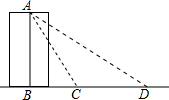 如图,要测量底部不能到达的一座塔的高度AB,甲、乙两名同学分别在C,D两处进行了测量.已知点B,C,D在同一直线上,且AB⊥BD,CD=12米,∠ACB=60°,∠ADB=30°,则塔的高度AB为( )
如图,要测量底部不能到达的一座塔的高度AB,甲、乙两名同学分别在C,D两处进行了测量.已知点B,C,D在同一直线上,且AB⊥BD,CD=12米,∠ACB=60°,∠ADB=30°,则塔的高度AB为( )| A. | 12$\sqrt{3}$米 | B. | 6$\sqrt{3}$米 | C. | 12米 | D. | 6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com