
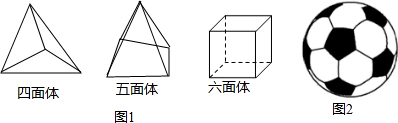
分析 (1)直接利用欧拉公式求出答案;
(2)根据题意可知:本题中的等量关系是“黑白皮块32块”和因为每块白皮有3条边与黑边连在一起,所以黑皮只有(32-x)块,而黑皮共有边数为5x块,依此借助欧拉公式列方程求解即可.
解答 解:(1)V+F-E=2.
故答案为:2;
(2)设正五边形有x块,则正六边形有32-x块,
则F=32,E=$\frac{5x+6(32-x)}{2}$=-$\frac{1}{2}$x+96,
V=E÷3×2=-$\frac{1}{3}$x+64,
根据欧拉公式得:V+F-E=2,
则-$\frac{1}{3}$x+64+32-(-$\frac{1}{2}$x+96)=2,
解得:x=12,32-x=20,
所以,正五边形有12块,正六边形有20块.
点评 此题主要考查了欧拉公式以及一元一次方程的应用,正确应用欧拉公式是解题关键.


科目:初中数学 来源: 题型:选择题
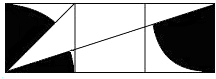 如图,方格纸中3个小正方形的边长均为1,则图中三个以1为半径的小扇形阴影部分的面积和为( )
如图,方格纸中3个小正方形的边长均为1,则图中三个以1为半径的小扇形阴影部分的面积和为( )| A. | $\frac{1}{3}π$ | B. | $\frac{3}{8}π$ | C. | $\frac{1}{2}π$ | D. | $\frac{2}{3}π$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
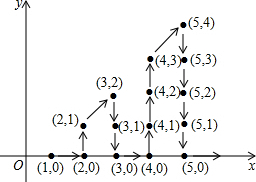 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…根据这个规律探索可得,第102个点的坐标为( )
如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…根据这个规律探索可得,第102个点的坐标为( )| A. | (13,8) | B. | (13,10) | C. | (14,8) | D. | (14,10) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
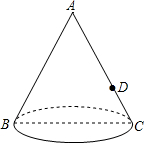 如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为2cm的等边△ABC,点D是AC的中点,一只蚂蚁从点B出发沿圆锥的表面爬行到点D处,则这只蚂蚁爬行的最短距离是$\sqrt{5}$cm.
如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为2cm的等边△ABC,点D是AC的中点,一只蚂蚁从点B出发沿圆锥的表面爬行到点D处,则这只蚂蚁爬行的最短距离是$\sqrt{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
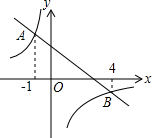 已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )| A. | x<-1或x>4 | B. | -1<x<4 | C. | x<-1或0<x<4 | D. | -1<x<0或x>4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com