
°æƒø°øœ ∑·ÀÆπ˚µÍº∆ªÆ”√![]() ‘™/∫–µƒΩ¯º€π∫Ω¯“ªøÓÀÆπ˚¿Ò∫–“‘±∏œ˙ €£Æ
‘™/∫–µƒΩ¯º€π∫Ω¯“ªøÓÀÆπ˚¿Ò∫–“‘±∏œ˙ €£Æ
![]() æðµ˜≤È£¨µ±∏√÷÷ÀÆπ˚¿Ò∫–µƒ €º€Œ™
æðµ˜≤È£¨µ±∏√÷÷ÀÆπ˚¿Ò∫–µƒ €º€Œ™![]() ‘™/∫– ±£¨‘¬œ˙¡øŒ™
‘™/∫– ±£¨‘¬œ˙¡øŒ™![]() ∫–£¨√ø∫– €º€√ø‘ˆ≥§
∫–£¨√ø∫– €º€√ø‘ˆ≥§![]() ‘™£¨‘¬œ˙¡øæÕœý”¶ºı…Ÿ
‘™£¨‘¬œ˙¡øæÕœý”¶ºı…Ÿ![]() ∫–£¨»Ù πÀÆπ˚¿Ò∫–µƒ‘¬œ˙¡ø≤ªµÕ”⁄
∫–£¨»Ù πÀÆπ˚¿Ò∫–µƒ‘¬œ˙¡ø≤ªµÕ”⁄![]() ∫–£¨√ø∫– €º€”¶≤ª∏þ ”⁄∂ý…Ÿ‘™£ø
∫–£¨√ø∫– €º€”¶≤ª∏þ ”⁄∂ý…Ÿ‘™£ø
![]() ‘⁄ µº œ˙ € ±£¨”…”⁄ÃÏ∆¯∫Õ‘À ‰µƒ‘≠“Ú£¨√ø∫–ÀÆπ˚¿Ò∫–µƒΩ¯º€Ã·∏þ¡À
‘⁄ µº œ˙ € ±£¨”…”⁄ÃÏ∆¯∫Õ‘À ‰µƒ‘≠“Ú£¨√ø∫–ÀÆπ˚¿Ò∫–µƒΩ¯º€Ã·∏þ¡À![]() £¨∂¯√ø∫– ÀÆπ˚¿Ò∫–µƒ €º€±»
£¨∂¯√ø∫– ÀÆπ˚¿Ò∫–µƒ €º€±»![]() ÷–◊Ó∏þ €º€ºı…Ÿ¡À
÷–◊Ó∏þ €º€ºı…Ÿ¡À![]()
![]() £¨‘¬œ˙¡ø±»
£¨‘¬œ˙¡ø±»![]() ÷–◊ÓµÕ‘¬œ˙¡ø
÷–◊ÓµÕ‘¬œ˙¡ø![]() ∫–‘ˆº”¡À
∫–‘ˆº”¡À![]() £¨Ω·π˚∏√‘¬ÀÆπ˚µÍœ˙ €∏√ÀÆπ˚¿Ò∫–µƒ¿˚»Û¥ÔµΩ¡À
£¨Ω·π˚∏√‘¬ÀÆπ˚µÍœ˙ €∏√ÀÆπ˚¿Ò∫–µƒ¿˚»Û¥ÔµΩ¡À![]() ‘™£¨«Û
‘™£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
°æ¥∞∏°ø£®1£©»Ù πÀÆπ˚¿Ò∫–µƒ‘¬œ˙¡ø≤ªµÕ”⁄![]() ∫–£¨√ø∫– €º€”¶≤ª∏þ”⁄
∫–£¨√ø∫– €º€”¶≤ª∏þ”⁄![]() ‘™£ª£®2£©
‘™£ª£®2£©![]() µƒ÷µŒ™
µƒ÷µŒ™![]() £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©…Ë√ø∫– €º€”¶Œ™x‘™£¨∏˘æ𑬜˙¡ø£Ω98030°¡≥¨≥ˆ14‘™µƒ≤ø∑÷Ω·∫œ‘¬œ˙¡ø≤ªµÕ”⁄800∫–£¨º¥ø…µ√≥ˆπÿ”⁄xµƒ“ª‘™“ª¥Œ≤ªµ» Ω£¨Ω‚÷Æ»°∆‰◊Ó¥Û÷µº¥ø…µ√≥ˆΩ·¬€£ª
£®2£©∏˘æð◊п˚»Û£Ω√ø∫–¿˚»Û°¡œ˙ € ˝¡ø£¨º¥ø…µ√≥ˆπÿ”⁄mµƒ“ª‘™∂˛¥Œ∑Ω≥ã¨Ω‚÷Æ»°∆‰’˝÷µº¥ø…µ√≥ˆΩ·¬€£Æ
Ω‚£∫![]() …Ë√ø∫– €º€
…Ë√ø∫– €º€ ![]() ‘™£Æ
‘™£Æ
“¿Ã‚“‚µ√£∫![]()
Ω‚µ√£∫![]()
¥£∫»Ù πÀÆπ˚¿Ò∫–µƒ‘¬œ˙¡ø≤ªµÕ”⁄![]() ∫–£¨√ø∫– €º€”¶≤ª∏þ”⁄
∫–£¨√ø∫– €º€”¶≤ª∏þ”⁄![]() ‘™
‘™
![]() “¿Ã‚“‚£∫
“¿Ã‚“‚£∫![]()
¡Ó£∫![]()
ªØºÚ£∫![]()
Ω‚µ√£∫![]() £®…·»•£©£¨
£®…·»•£©£¨![]()
![]()
¥£∫![]() µƒ÷µŒ™
µƒ÷µŒ™![]() £Æ
£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄µ»—¸Rt°˜ABC÷–£¨°œC=90°„£¨AC=4£¨æÿ–ŒDEFGµƒ∂•µ„D°¢G∑÷±‘⁄AC°¢BC…œ£¨±þEF‘⁄AB…œ£Æ
£®1£©«Û÷§£∫°˜AED°◊°˜DCG£ª
£®2£©»Ùæÿ–ŒDEFGµƒ√ʪ˝Œ™4£¨«ÛAEµƒ≥§£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
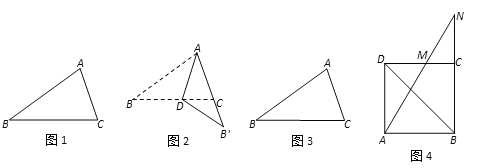
°æƒø°ø‘ƒ∂¡≤ƒ¡œ£∫µ»—¸»˝Ω«–Œæþ”––‘÷ °∞µ»±þ∂‘µ»Ω«°±£Æ ¬ µ…œ£¨≤ªµ»±þ»˝Ω«–Œ“≤æþ”–¿ýÀ∆–‘÷ °∞¥Û±þ∂‘¥ÛΩ«°±£∫»ÁÕº1£Æ‘⁄°˜ABC÷–£¨»Áπ˚AB£æAC£¨ƒ«√¥°œACB£æ°œABC£Æ÷§√˜»Áœ¬£∫Ω´AB—ÿ°˜ABCµƒΩ«∆Ω∑÷œþAD∑≠’€£®»ÁÕº2£©£¨“ÚŒ™AB£æAC£¨À˘“‘µ„B¬‰‘⁄ACµƒ—”≥§œþ…œµƒµ„B'¥¶£Æ”⁄ «£¨”…°œACB£æ°œB'£¨°œABC=°œB'£¨ø…µ√°œACB£æ°œABC£Æ
£®1£©¡ÈªÓ‘À”√£∫¥”…œ√ʵƒ÷§∑®ø…“‘ø¥≥ˆ£¨’€÷Ω≥£≥£ƒÐŒ™÷§√˜“ª∏ˆ√¸Ã‚÷π©Àº¬∑∫Õ∑Ω∑®£Æ”…¥À–°√˜œÎµΩø…”√¿ýÀ∆∑Ω∑®÷§√˜°∞¥ÛΩ«∂‘¥Û±þ°±£∫»ÁÕº3£Æ‘⁄°˜ABC÷–£¨»Áπ˚°œACB£æ°œABC£¨ƒ«√¥AB£æAC£Æ–°√˜µƒÀº¬∑ «£∫—ÿBCµƒ¥π÷±∆Ω∑÷œþ∑≠’€°≠°≠«Îƒ„∞Ô÷˙–°√˜ÕÍ≥…∫Û√ʵƒ÷§√˜π˝≥ãÆ
£®2£©Õÿ’π—”…Ï£∫«Î‘À”√…œ ˆ∑Ω∑®ªÚΩ·¬€Ω‚戻Áœ¬Œ £∫
»ÁÕº4£¨“—÷™MŒ™’˝∑Ω–ŒABCDµƒ±þCD…œ“ªµ„£®≤ª∫¨∂Àµ„£©£¨¡¨Ω”AM≤¢—”≥§£¨ΩªBCµƒ—”≥§œþ”⁄µ„N£Æ«Û÷§£∫AM£´AN£æ2BD£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
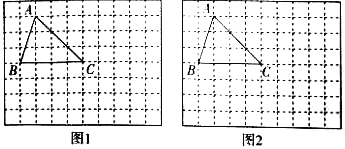
°æƒø°ø»ÁÕº£¨‘⁄”…±þ≥§Œ™1∏ˆµ•Œª≥§∂»µƒ–°’˝∑Ω–Œ◊È≥…µƒÕ¯∏ÒÕº÷–”–∏Òµ„°˜ABC(◊¢:∂•µ„‘⁄Õ¯∏ÒœþΩªµ„¥¶µƒ»˝Ω«–ŒΩ–◊ˆ∏Òµ„»˝Ω«–Œ)£Æ÷ª”√√ª”–øÃ∂»µƒ÷±≥þ£¨∞¥»Áœ¬“™«Ûª≠Õº£¨
(1)“‘µ„CŒ™ŒªÀ∆÷––ƒ£¨‘⁄»ÁÕº÷–◊˜°˜DEC°◊ABC£¨«“œýÀ∆±»Œ™1:2;
(2)»Ùµ„BŒ™‘≠µ„£¨µ„C(4,0),«Î‘⁄»ÁÕº÷–ª≠≥ˆ∆Ω√Ê÷±Ω«◊¯±Íœµ£¨◊˜≥ˆ°˜ABCµƒÕ‚–ƒ,≤¢÷±Ω”–¥≥ˆ°˜ABCµƒÕ‚–ƒµƒ◊¯±Í
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
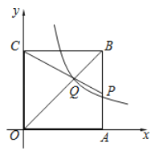
°æƒø°ø»ÁÕº£¨’˝∑Ω–Œµƒ±þ≥§Œ™![]() ∑÷±Œª”⁄
∑÷±Œª”⁄![]() ÷·£¨
÷·£¨![]() ÷·…œ£¨µ„
÷·…œ£¨µ„![]() ‘⁄
‘⁄![]() …œ£¨
…œ£¨![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨∫Ø ˝
£¨∫Ø ˝![]() µƒÕºœÒæ≠π˝µ„
µƒÕºœÒæ≠π˝µ„![]() £¨»Ù
£¨»Ù![]() £¨‘Ú
£¨‘Ú![]() µƒ÷µŒ™£® £©
µƒ÷µŒ™£® £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øµ˜≤È◊˜“µ£∫¡ÀΩ‚ƒ„À˘◊°–°«¯º“Õ•3‘¬∑ð”√∆¯¡ø«Èøˆ£Æ
–°ÃÏ°¢–°∂´∫Õ–°Ðø»˝ŒªÕ¨—ß◊°‘⁄Õ¨“ª–°«¯£¨∏√–°«¯π≤”–300ªßº“Õ•£¨√øªßº“Õ•»À ˝‘⁄2°™5÷ƺ‰£¨’‚300ªßº“Õ•µƒ∆Ωæ˘»À ˝‘ºŒ™3.3£Æ
–°ÃÏ°¢–°∂´∫Õ–°Ðø∏˜◊‘∂‘∏√–°«¯º“Õ•3‘¬∑ð”√∆¯¡ø«ÈøˆΩ¯––¡À≥È—˘µ˜≤È£¨Ω´ ’ºØµƒ ˝æðΩ¯––¡À’˚¿Ì£¨ªÊ÷∆µƒÕ≥º∆±Ì∑÷±Œ™±Ì1°¢±Ì2°¢±Ì3£¨
±Ì1≥È—˘µ˜≤È–°«¯4ªßº“Õ•3‘¬∑ð”√∆¯¡øÕ≥º∆±Ì£®µ•Œª£∫![]() £©
£©
º“Õ•»À ˝ | 2 | 3 | 4 | 5 |
”√∆¯¡ø | 14 | 19 | 21 | 26 |
±Ì2≥È—˘µ˜≤È–°«¯15ªßº“Õ•3‘¬∑ð”√∆¯¡øÕ≥º∆±Ì£®µ•Œª£∫![]() £©
£©
º“Õ•»À ˝ | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
”√∆¯¡ø | 10 | 11 | 15 | 13 | 14 | 15 | 17 | 17 | 18 | 18 | 18 | 18 | 18 | 20 | 22 |
±Ì3≥È—˘µ˜≤È–°«¯15ªßº“Õ•3‘¬∑ð”√∆¯¡øÕ≥º∆±Ì£®µ•Œª£∫![]() £©
£©
º“Õ•»À ˝ | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
”√∆¯¡ø | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
∏˘æð“‘…œ≤ƒ¡œªÿ¥Œ £∫
£®1£©–°ÃÏ°¢–°∂´∫Õ–°Ðø»˝»À÷–£¨ƒƒ“ªŒªÕ¨—ß≥È—˘µ˜≤ȵƒ ˝æðƒÐΩœ∫√µÿ∑¥”¶≥ˆ∏√–°«¯º“Õ•3‘¬∑ð”√∆¯¡ø«Èøˆ£ø«ÎºÚ“™Àµ√˜∆‰À˚¡ΩŒªÕ¨—ß≥È—˘µ˜≤ȵƒ≤ª◊„÷Æ¥¶£ª
£®2£©–°∂´Ω´±Ì2÷–µƒ ˝æð∞¥”√∆¯¡ø![]() ¥Û–°∑÷Œ™»˝¿ý£ª
¥Û–°∑÷Œ™»˝¿ý£ª
¢ŸΩ⁄‘º–Õ£∫![]() £ª
£ª
¢⁄æ”÷––Õ£∫![]() £ª
£ª
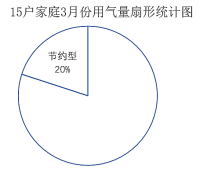
¢€∆´∏þ–Õ£∫![]() £ª≤¢ªÊ÷∆≥…»Áœ¬…»–ŒÕ≥º∆Õº£¨«Î∞Ô÷˙À˚Ω´…»–ŒÕº≤π≥‰ÕÍ’˚£ª
£ª≤¢ªÊ÷∆≥…»Áœ¬…»–ŒÕ≥º∆Õº£¨«Î∞Ô÷˙À˚Ω´…»–ŒÕº≤π≥‰ÕÍ’˚£ª
£®3£©–°ÐøÀ„≥ˆ±Ì3÷–3‘¬∑ð∆Ωæ˘√ø»Àµƒ”√¡øŒ™![]() £¨«Îπ¿º∆∏√–°«¯3‘¬∑ðµƒ◊Д√∆¯¡ø£Æ
£¨«Îπ¿º∆∏√–°«¯3‘¬∑ðµƒ◊Д√∆¯¡ø£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨∫Ø ˝ y kx ”Î y  µƒÕºœÛΩª”⁄ A°¢B ¡Ωµ„£¨π˝ A ◊˜ y ÷·µƒ¥πœþ£¨Ωª∫Ø ˝
µƒÕºœÛΩª”⁄ A°¢B ¡Ωµ„£¨π˝ A ◊˜ y ÷·µƒ¥πœþ£¨Ωª∫Ø ˝ µƒÕºœÛ”⁄µ„ C£¨¡¨Ω” BC£¨‘Ú°˜ABC µƒ√ʪ˝Œ™£® £©
µƒÕºœÛ”⁄µ„ C£¨¡¨Ω” BC£¨‘Ú°˜ABC µƒ√ʪ˝Œ™£® £©

A. 2 B. 4 C. 6 D. 8
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº«ƒ≥…Ã∆∑œ˙ €µ•º€Œ™x‘™£¨…ú“œ˙ €¥À÷÷…Ã∆∑√ø‘¬ªÒµ√µƒœ˙ €¿˚»ÛŒ™y‘™£¨«“y «πÿ”⁄xµƒ∂˛¥Œ∫Ø ˝£Æ“—÷™µ±…ú“Ω´¥À÷÷…Ã∆∑œ˙ €µ•º€∑÷±∂®Œ™55‘™ªÚ75‘™ ±£¨À˚√ø‘¬æ˘ø…ªÒµ√œ˙ €¿˚»Û1800‘™£ªµ±…ú“Ω´¥À÷÷…Ã∆∑œ˙ €µ•º€∂®Œ™80‘™ ±£¨À˚√ø‘¬ø…ªÒµ√œ˙ €¿˚»Û1550‘™£¨‘Úy”Îxµƒ∫Ø ˝πÿœµ Ω «£® £©
A.y£Ω©Å£®x©Å60£©2+1825B.y£Ω©Å2£®x©Å60£©2+1850
C.y£Ω©Å£®x©Å65£©2+1900D.y£Ω©Å2£®x©Å65£©2+2000
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
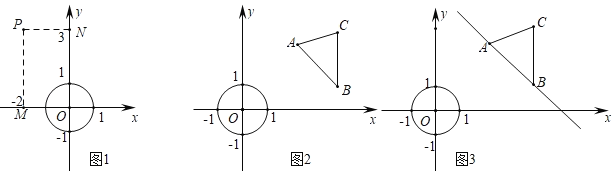
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy£¨∂‘”⁄µ„P£®xp£¨yp£©∫ÕÕº–ŒG£¨…ËQ£®xQ£¨yQ£© «Õº–ŒG…œ»Œ“‚“ªµ„£¨|xp©ÅxQ|µƒ◊Ó–°÷µΩ–µ„P∫ÕÕº–ŒGµƒ°∞ÀÆ∆Ωæý¿Î°±£¨|yp©ÅyQ|µƒ◊Ó–°÷µΩ–µ„P∫ÕÕº–ŒGµƒ°∞ ˙÷±æý¿Î°±£¨µ„P∫ÕÕº–ŒGµƒ°∞ÀÆ∆Ωæý¿Î°±”ΰ∞ ˙÷±æý¿Î°±µƒ◊Ó¥Û÷µΩ–◊ˆµ„P∫ÕÕº–ŒGµƒ°∞æ¯∂‘æý¿Î°±
¿˝»Á£∫µ„P£®©Å2£¨3£©∫Õ∞Îæ∂Œ™1µƒ°—O£¨“ÚŒ™°—O…œ»Œ“ªµ„Q£®xQ£¨yQ£©¬˙◊„©Å1°ÐxQ°Ð1£¨©Å1°ÐyQ°Ð1£¨µ„P∫Õ°—Oµƒ°∞ÀÆ∆Ωæý¿Î°±Œ™|©Å2©ÅxQ|µƒ◊Ó–°÷µ£¨º¥|©Å2©Å£®©Å1£©|=1£¨µ„P∫Õ°—Oµƒ°∞ ˙÷±æý¿Î°±Œ™|3©ÅyQ|µƒ◊Ó–°÷µº¥|3©Å1|=2£¨“ÚŒ™2£æ1£¨À˘“‘µ„P∫Õ°—Oµƒ°∞æ¯∂‘æý¿Î°±Œ™2£Æ
“—÷™°—O∞Îæ∂Œ™1£¨A£®2£¨![]() £©£¨B£®4£¨1£©£¨C£®4£¨3£©
£©£¨B£®4£¨1£©£¨C£®4£¨3£©
£®1£©¢Ÿ÷±Ω”–¥≥ˆµ„A∫Õ°—Oµƒ°∞æ¯∂‘æý¿Î°±
¢⁄“—÷™D «°˜ABC±þ…œ“ª∏ˆ∂ص„£¨µ±µ„D”ΰ—Oµƒ°∞æ¯∂‘æý¿Î°±Œ™2 ±£¨–¥≥ˆ“ª∏ˆ¬˙◊„Ãıº˛µƒµ„Dµƒ◊¯±Í£ª
£®2£©“—÷™E «°˜ABC±þ“ª∏ˆ∂ص„£¨÷±Ω”–¥≥ˆµ„E”ΰ—Oµƒ°∞æ¯∂‘æý¿Î°±µƒ◊Ó–°÷µº∞œý”¶µƒµ„Eµƒ◊¯±Í
£®3£©“—÷™P «°—O…œ“ª∏ˆ∂ص„£¨°˜ABC—ÿ÷±œþAB∆Ω“∆π˝≥Ã÷–£¨÷±Ω”–¥≥ˆµ„P”ΰ˜ABCµƒ°∞æ¯∂‘æý¿Î°±µƒ◊Ó–°÷µº∞œý”¶µƒµ„P∫Õµ„Cµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com