
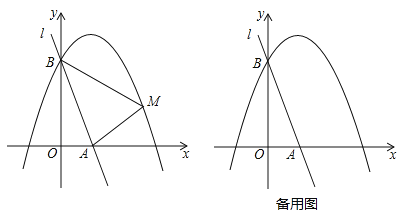
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线![]() (a<0)经过点B.
(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
【答案】(1)![]() ;(2)S=
;(2)S=![]() ,当m=
,当m=![]() 时,S取得最大值
时,S取得最大值![]() ;(3)①M′(
;(3)①M′(![]() ,
,![]() );②45°.
);②45°.
【解析】
试题分析:(1)利用直线l的解析式求出B点坐标,再把B点坐标代入二次函数解析式即可求出a的值;
(2)设M的坐标为(m,![]() ),然后根据面积关系将△ABM的面积进行转化;
),然后根据面积关系将△ABM的面积进行转化;
(3)①由(2)可知m=![]() ,代入二次函数解析式即可求出纵坐标的值;
,代入二次函数解析式即可求出纵坐标的值;
②可将求d1+d2最大值转化为求AC的最小值.
试题解析:(1)令x=0代入y=﹣3x+3,∴y=3,∴B(0,3),把B(0,3)代入![]() ,∴3=a+4,∴a=﹣1,∴二次函数解析式为:
,∴3=a+4,∴a=﹣1,∴二次函数解析式为:![]() ;
;
(2)令y=0代入![]() ,∴
,∴![]() ,∴x=﹣1或3,∴抛物线与x轴的交点横坐标为﹣1和3,∵M在抛物线上,且在第一象限内,∴0<m<3,令y=0代入y=﹣3x+3,∴x=1,∴A的坐标为(1,0),由题意知:M的坐标为(m,
,∴x=﹣1或3,∴抛物线与x轴的交点横坐标为﹣1和3,∵M在抛物线上,且在第一象限内,∴0<m<3,令y=0代入y=﹣3x+3,∴x=1,∴A的坐标为(1,0),由题意知:M的坐标为(m,![]() ),S=S四边形OAMB﹣S△AOB
),S=S四边形OAMB﹣S△AOB
=S△OBM+S△OAM﹣S△AOB=![]() ×m×3+
×m×3+![]() ×1×(
×1×(![]() )﹣
)﹣![]() ×1×3=
×1×3=![]() ,∵S=
,∵S=![]() =
=![]() ,∴当m=
,∴当m=![]() 时,S取得最大值
时,S取得最大值![]() .
.

(3)①由(2)可知:M′的坐标为(![]() ,
,![]() );
);
②过点M′作直线l1∥l′,过点B作BF⊥l1于点F,根据题意知:d1+d2=BF,此时只要求出BF的最大值即可,∵∠BFM′=90°,∴点F在以BM′为直径的圆上,设直线AM′与该圆相交于点H,∵点C在线段BM′上,∴F在优弧![]() 上,∴当F与M′重合时,BF可取得最大值,此时BM′⊥l1,∵A(1,0),B(0,3),M′(
上,∴当F与M′重合时,BF可取得最大值,此时BM′⊥l1,∵A(1,0),B(0,3),M′(![]() ,
,![]() ),∴由勾股定理可求得:AB=
),∴由勾股定理可求得:AB=![]() ,M′B=
,M′B=![]() ,M′A=
,M′A=![]() ,过点M′作M′G⊥AB于点G,设BG=x,∴由勾股定理可得:
,过点M′作M′G⊥AB于点G,设BG=x,∴由勾股定理可得:![]() ,∴
,∴![]() ,∴x=
,∴x=![]() ,cos∠M′BG=
,cos∠M′BG=![]() =
=![]() ,∵l1∥l′,∴∠BCA=90°,∠BAC=45°;
,∵l1∥l′,∴∠BCA=90°,∠BAC=45°;

方法二:过B点作BD垂直于l′于D点,过M点作ME垂直于l′于E点,则BD=d1,ME=d2,∵S△ABM=![]() ×AC×(d1+d2),当d1+d2取得最大值时,AC应该取得最小值,当AC⊥BM时取得最小值.
×AC×(d1+d2),当d1+d2取得最大值时,AC应该取得最小值,当AC⊥BM时取得最小值.
根据B(0,3)和M′(![]() ,
,![]() )可得BM′=
)可得BM′=![]() ,∵S△ABM=
,∵S△ABM=![]() ×AC×BM′=
×AC×BM′=![]() ,∴AC=
,∴AC=![]() ,当AC⊥BM′时,cos∠BAC=
,当AC⊥BM′时,cos∠BAC=![]() =
=![]() =
=![]() ,∴∠BAC=45°.
,∴∠BAC=45°.



科目:初中数学 来源: 题型:
【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为:
 ,且其日销售量y(kg)与时间t(天)的关系如下表:
,且其日销售量y(kg)与时间t(天)的关系如下表:

(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
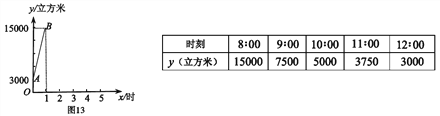
【题目】为节约能源,某市众多车主响应号召,将燃油汽车改装为天然气汽车.某日上午7:00-8:00, 燃气公司给该城西加气站的储气罐加气,8:00 加气站开始为前来的车辆加气. 储气罐内的天然气总量y(立方米)随加气时间x(时)的变化而变化.
(1)在7:00-8:00 范围内,y 随x的变化情况如图13 所示,求y 关于x 的函数解析式;
(2)在8:00-12:00 范围内,y 的变化情况如下表所示,请写出一个符合表格中数据的y 关于x 的函数解析式,依此函数解析式,判断上午9:05 到9:20 能否完成加气950 立方米的任务,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( ) 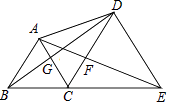
A.△ACE≌△BCD
B.△BGC≌△AFC
C.△ADB≌△CEA
D.△DCG≌△ECF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com