
【题目】东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为:
 ,且其日销售量y(kg)与时间t(天)的关系如下表:
,且其日销售量y(kg)与时间t(天)的关系如下表:

(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
【答案】(1)y=120-2t,60;(2)在第10天的销售利润最大,最大利润为1250元;(3)7≤n<9.
【解析】
试题分析:(1)根据日销售量y(kg)与时间t(天)的关系表,设y=kt+b,将表中对应数值代入即可求出k,b,从而求出一次函数关系式,再将t=30代入所求的一次函数关系式中,即可求出第30天的日销售量.
(2)日销售利润=日销售量×(销售单价-成本);分1≤t≤24和25≤t≤48两种情况,按照题目中所给出的销售单价p(元/kg)与时间t(天)之间的函数关系式分别得出销售利润的关系式,再运用二次函数的图像及性质即可得出结果.
(3)根据题意列出日销售利润W=(t+30-20-n)(120-2t)= -t2+2(n+5)t+1200-n,此二次函数的对称轴为y=2n+10,要使W随t的增大而增大,2n+10≥24,即可得出n的取值范围.
试题解析:(1)依题意,设y=kt+b,将(10,100),(20,80)代入y=kt+b,得:![]() ,解得:
,解得:![]() ,∴日销售量y(kg)与时间t(天)的关系 y=120-2t.当t=30时,y=120-60=60.
,∴日销售量y(kg)与时间t(天)的关系 y=120-2t.当t=30时,y=120-60=60.
答:在第30天的日销售量为60千克.
(2)设日销售利润为W元,则W=(p-20)y.
当1≤t≤24时,W=(t+30-20)(120-t)=![]() =
=![]()
当t=10时,W最大=1250.
当25≤t≤48时,W=(-t+48-20)(120-2t)=![]() =
=![]()
由二次函数的图像及性质知:当t=25时,W最大=1085.
∵1250>1085,∴在第10天的销售利润最大,最大利润为1250元.
(3)依题意,得:W=(t+30-20-n)(120-2t)= ![]() ,其对称轴为y=2n+10,要使W随t的增大而增大,由二次函数的图像及性质知:2n+10≥24,解得n≥7.
,其对称轴为y=2n+10,要使W随t的增大而增大,由二次函数的图像及性质知:2n+10≥24,解得n≥7.
又∵n<0,∴7≤n<9.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式(也称关系式);
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
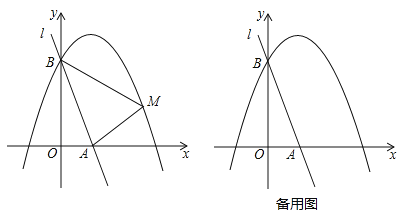
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线![]() (a<0)经过点B.
(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用科学记数法表示一个数字的一般形式为a×10n,其中对字母a和n都有要求,那么对于a的要求是( )
A.a必须是整数
B.a必须是正整数
C.a必须是有理数
D.a的取值范围是大于等于1且小于10的有理数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).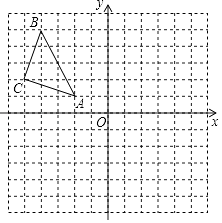
(1)画出△ABC关于y对称的△A1B1C1 , 其中,点A、B、C的对应点分别为A1、B1、C1;
(2)直接写出点A1、B1、C1的坐标; A1 , B1 , C1 .
(3)△A1B1C1的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN. 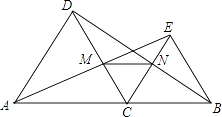
(1)求证:AE=BD;
(2)求证:MN∥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把代数式mx2-6mx+9m分解因式,下列结果中正确的是( )
A.m(x+3)2
B.m(x+3)(x-3)
C.m(x-4)2
D.m(x-3)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各因式分解正确的是( )
A. x2+2x-1=(x-1)2
B. -x2+(-2)2=(x-2)(x+2)
C. x3-4x = x(x+2)(x-2)
D. (x+1)2= x2+2x+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com