
【题目】为节约能源,某市众多车主响应号召,将燃油汽车改装为天然气汽车.某日上午7:00-8:00, 燃气公司给该城西加气站的储气罐加气,8:00 加气站开始为前来的车辆加气. 储气罐内的天然气总量y(立方米)随加气时间x(时)的变化而变化.
(1)在7:00-8:00 范围内,y 随x的变化情况如图13 所示,求y 关于x 的函数解析式;
(2)在8:00-12:00 范围内,y 的变化情况如下表所示,请写出一个符合表格中数据的y 关于x 的函数解析式,依此函数解析式,判断上午9:05 到9:20 能否完成加气950 立方米的任务,并说明理由.
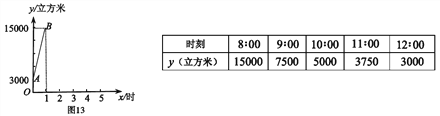
【答案】(1)在8:00-8:00范围内,y关于x的函数解析式为:y=12000x+3000(0≤x≤1)
(2)上午9:05到9:20不能完成加气950立方米的任务
【解析】试题分析:(1)根据图象发现是一次函数,把点A(0,3000),B(1,15000)代入即可求解;(2)因为y随x的增大而减小,所以猜测是反比例函数y=![]() (1≤x≤3),根据x=1时,y=15000,即上午8:00,x与y的值满足解析式,再验证其余时间是否满足, 把上午9:05即x=2
(1≤x≤3),根据x=1时,y=15000,即上午8:00,x与y的值满足解析式,再验证其余时间是否满足, 把上午9:05即x=2![]() 时代入y=
时代入y=![]() (1≤x≤3)求出,再把上午9:20即x=2
(1≤x≤3)求出,再把上午9:20即x=2![]() 时代入y=
时代入y=![]() (1≤x≤3)求出,两结果之差和950进行比较就能得出结果.
(1≤x≤3)求出,两结果之差和950进行比较就能得出结果.
试题解析:
(1)设直线AB的解析式为y=kx+b,
把点A(0,3000),B(1,15000)分别代入,得
k=12000,b=3000.
在8:00-8:30范围内,y关于x的函数解析式为:y=12000x+3000(0≤x≤1).
(2)解法一:函数解析式为:y=![]() (1≤x≤3).
(1≤x≤3).
验证如下:
当x=1时,y=15000,即上午8:00,x与y的值满足解析式.
同理,表格数据所对应的x与y的值都满足解析式.
当上午9:05即x=2![]() 时,y=7200立方米.
时,y=7200立方米.
当上午9:20即x=2![]() 时,y=
时,y=![]() 立方米.
立方米.
∵ 7200-![]() =
=![]() ,
,
又∵![]() <950,
<950,
∴ 上午9:05到9:20不能完成加气950立方米的任务.
解法二:函数解析式为:y=![]() (1≤x≤3).
(1≤x≤3).
验证如下:
当x=1时,y=15000,即上午8:00,x与y的值满足解析式.
同理,表格数据所对应的x与y的值都满足解析式.
当上午9:05即x=2![]() 时,y=7200立方米.
时,y=7200立方米.
7200-950=6250.
当y=6250立方米,x=2![]() 时.
时.
即到上午9:24才可完成加气任务.
所以上午9:05到9:20不能完成加气950立方米的任务.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
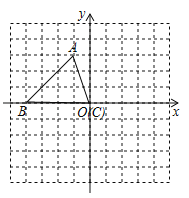
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
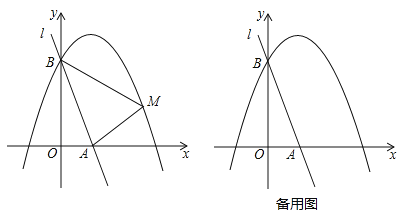
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线![]() (a<0)经过点B.
(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).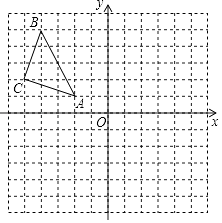
(1)画出△ABC关于y对称的△A1B1C1 , 其中,点A、B、C的对应点分别为A1、B1、C1;
(2)直接写出点A1、B1、C1的坐标; A1 , B1 , C1 .
(3)△A1B1C1的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN. 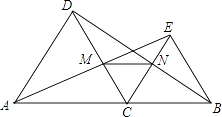
(1)求证:AE=BD;
(2)求证:MN∥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红骑车从家出发,先向东骑行2km到达A村,继续向东骑行3km到达B村,然后向西骑行8km到达C村,最后回到家.
(1)以家为原点,以向东方向为正方向,用1cm表示1km,画出数轴,并在数轴上表示出A、B、C三个村庄的位置;
(2)C村离A村有多远?(直接写出答案)
(3)小红一共行了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把代数式mx2-6mx+9m分解因式,下列结果中正确的是( )
A.m(x+3)2
B.m(x+3)(x-3)
C.m(x-4)2
D.m(x-3)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,2015年第一季度,广东省实现地区生产总值约1560 000 000 000元,用科学记数法表示为( )
A.0.156×1012元
B.1.56×1012元
C.1.56×1011元
D.15.6×1011元
查看答案和解析>>
科目:初中数学 来源: 题型:
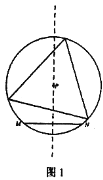
【题目】定义:如图l所示,给定线段MN及其垂直平分线上一点P。若以点P为圆心,PM为半径的优弧(或半圆弧)MN上存在三个点可以作为一个等边三角形的顶点,则称点P为线段MN的“三足点”,特别的,若这样的等边三角形只存在一个,则称点P为线段MN的“强三足点”。
问题:如图2所示,平面直角坐标系xOy中,点A的坐标为(2![]() ,0),点B在射线y=
,0),点B在射线y=![]() x(x≥0)上。
x(x≥0)上。
(1)在点C(![]() ,0),D(
,0),D(![]() ,1),E(
,1),E(![]() ,-2)中,可以成为线段OA的“三足点”的是__________.
,-2)中,可以成为线段OA的“三足点”的是__________.
(2)若第一象限内存在一点Q既是线段OA的“三足点”,又是线段OB的“强三足点”,求点B的坐标。
(3)在(2)的条件下,以点A为圆心,AB为半径作圆,假设该圆与x轴交点中右侧一个为H,圆上一动点K从H出发,绕A顺时针旋转180°后停止,设点K出发后转过的角度为![]() (0°<
(0°< ![]() ≤180°),若线段OB与AK不存在公共“三足点”,请直接写出
≤180°),若线段OB与AK不存在公共“三足点”,请直接写出![]() 的取值范围是_______________。
的取值范围是_______________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com