练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】“皮影戏”作为我国一种民间艺术，对它的叙述错误的是（ ）

    A. 它是用兽皮或纸板做成的人物剪影，来表演故事的戏曲

    B. 表演时，要用灯光把剪影照在银幕上

    C. 灯光下，做不同的手势可以形成不同的手影

    D. 表演时，也可用阳光把剪影照在银幕上

    【答案】D

    【解析】

    本题考查的是中心投影的性质

    解答本题的关键是了解“皮影戏”，“皮影戏”是我国的民间故事表演，它是用兽皮或纸板做成的人物剪影，来表演故事的戏曲，演时，要用灯光把剪影照在银幕上，灯光下，做不同的手势可以形成不同的手影，但是不能用阳光，“皮影戏”利用的是中心投影的性质，阳光是平行投影．

    “皮影戏”是我国的民间故事表演，它是用兽皮或纸板做成的人物剪影，来表演故事的戏曲，演时，要用灯光把剪影照在银幕上，灯光下，做不同的手势可以形成不同的手影，这些都是“皮影戏”的常识，故A、B、C都是正确的．

    “皮影戏”利用的是中心投影的原理，

    把光由一点向外散射形成的投影，叫做中心投影．中心投影的投影线交于一点．空间图形经过中心投影后、直线变成直线、但平行线可能变成了相交的直线，“皮影戏”正是利用了这一点，而阳光是平行投影，

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】抛物线y=x2﹣3x+4与x轴的交点个数为（ ）
    A.零个
    B.一个
    C.两个
    D.三个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】北方某水果商店从南方购进一种水果，其进货成本是每吨0.4万元，根据市场调查，这种水果在北方市场上的销售量为 y(吨)，销售价 x( 万元)之间的函数关系为y=-x+2.6.

    (1)当每吨销售价为多少万元时，销售利润为 0.96万元?

    (2)填空 当每吨销售价为 万元时，可得最大利润为 万元.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对下列各式进行因式分解：

    （1）2x(a-b)-(b-a)； （2）x4-9x2；

    （3）2mx2-4mxy+2my2； （4）a2-a-6.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某区今年共有1.4万名七年级学生参加期末考试，为了了解这1.4万名学生的数学成绩，从中抽取了1000名学生的数学成绩进行统计分析，以下说法正确的有（ ）个

    ①这种抽查采用了抽样调查的方式

    ②1.4万名学生的数学成绩是总体

    ③1000名学生是总体的一个样本

    ④每名学生的数学成绩是总体的一个样本．

    A. 4 B. 3 C. 2 D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

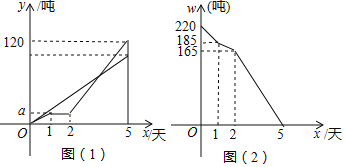
    【题目】某市制米厂接到加工大米任务，要求5天内加工完220吨大米，制米厂安排甲、乙两车间共同完成加工任务，乙车间加工中途停工一段时间维修设备，然后改变加工效率继续加工，直到与甲车间同时完成加工任务为止．设甲、乙两车间各自加工大米数量y（吨）与甲车间加工时间s（天）之间的关系如图（1）所示；未加工大米w（吨）与甲加工时间x（天）之间的关系如图（2）所示，请结合图象回答下列问题：

    （1）甲车间每天加工大米　 　吨，a=　 　．

    （2）求乙车间维修设备后，乙车间加工大米数量y（吨）与x（天）之间函数关系式．

    （3）若55吨大米恰好装满一节车厢，那么加工多长时间装满第一节车厢？再加工多长时间恰好装满第二节车厢？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，边AE上有一动点P（不与A，E重合）自A点沿AE方向向E点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为t秒（0＜t＜5），过P点作ED的平行线交AD于点M，过点M作AE的平行线交DE于点N．

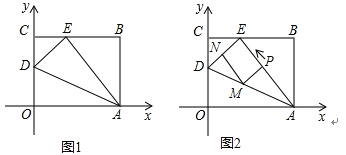
    （1）直接写出 D，E 两点的坐标，D（ ），E（ ）

    （2）求四边形PMNE的面积S与时间t之间的函数关系式；当t取何值时，S有最大值？

    （3）当t为何值时，DP平分∠EDA？

    （4）当t为何值时，以A，M，E为顶点的三角形为等腰三角形，并求出相应的时刻点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】回答下列问题：

    （1）如图所示的甲、乙两个平面图形能折成什么几何体？________________．

    （2）由多个平面围成的几何体叫做多面体．若一个多面体的面数为，顶点个数为，棱数为，分别计算第（1）题中两个多面体的的值？你发现什么规律？

    （3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1是立方体和长方体模型，立方体棱长和长方体底面各边长都为1，长方体侧棱长为2，现用60张长为6，宽为4的长方形卡纸，剪出这两种模型的表面展开图，有两种方法：

    方法一：如图2，每张卡纸剪出3个立方体表面展开图；

    方法二：如图3，每张卡纸剪出2个长方体表面展开图（图中只画出1个）．

    设用x张卡纸做立方体，其余卡纸做长方体，共做两种模型y个．要求制作的长方体的个数不超过立方体的个数．

    （1）在图3中画出第二个长方体表面展开图，用阴影表示；

    （2）请你写出y关于x的函数解析式，并注明自变量x的取值范围；

    （3）设每只模型（包括立方体和长方体）平均获利为w（元），w满足函数，

    若想将模型作为教具卖出获得最大利润，则应该制作立方体和长方体各多少个？最大利润是多少？

    查看答案和解析>>

    同步练习册答案