
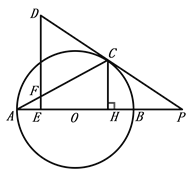
【题目】如图,AB为⊙O直径,过⊙O外的点D作DE⊥OA于点E,射线DC切⊙O于点C、交AB的延长线于点P,连接AC交DE于点F,作CH⊥AB于点H.
(1)求证:∠D=2∠A;
(2)若HB=2,cosD=![]() ,请求出⊙O的半径长.
,请求出⊙O的半径长.
【答案】(1)见解析;(2)5.
【解析】分析:(1)连接OC,根据切线的性质得到∠OCP=90°,根据垂直的定义得到∠DEP=90°,得到∠COB=∠D,根据圆周角定理证明;
(2)设⊙O的半径为r,根据余弦的定义计算即可.
详解:
(1)证明:连接OC,
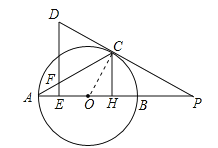
∵射线DC切⊙O于点C, ∴∠OCP=90°
∵DE⊥AP,∴∠DEP=90°
∴∠P+∠D=90°,∠P+∠COB=90°
∴∠COB=∠D
∵OA=OC, ∴∠A=∠OCA
∵∠COB=∠A+∠OCA ∴∠COB=2∠A
∴∠D=2∠A
(2)解:由(1)可知:∠OCP=90°,∠COP=∠D,
∴cos∠COP=cos∠D=![]() ,
,
∵CH⊥OP,∴∠CHO=90°,
设⊙O的半径为r,则OH=r﹣2.
在Rt△CHO中,cos∠HOC=![]() =
=![]() =
=![]() ,
,
∴r=5


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市,第23题,10分)湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批淡水鱼放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为![]() ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.
①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“水是生命之源”,某市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
用水量/月 | 单价(元/m3) |
不超过20m3 | 2.8 |
超过20m3的部分 | 3.8 |
另:每立方米用水加收0.2元的城市污水处理费 | |
(1)根据上表,用水量每月不超过20m3,实际每立方米收水费_____元;如果1月份某用户用水量为19m3,那么该用户1月份应该缴纳水费____元;
(2)某用户2月份共缴纳水费80元,那么该用户2月份用水多少m3?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,问该用户3月份实际应该缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D。
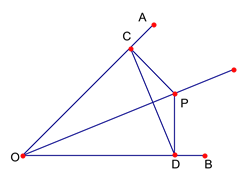
(1)求证:∠PCD=∠PDC;(2)求证:OP垂直平分线段CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD,OE分别是∠AOC,∠BOC的角平分线,下列叙述正确的是( )

A. ∠AOD+∠BOE=60°B. ∠AOD=![]() ∠EOC
∠EOC
C. ∠BOE=2∠CODD. ∠DOE的度数不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
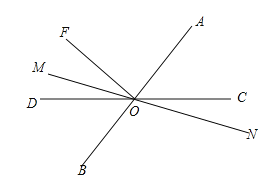
【题目】如图,直线AB、CD、MN相交与点O,FO⊥BO,OM平分∠DOF
(1)请直接写出图中所有与∠AON互余的角: .
(2)若∠AOC=![]() ∠FOM,求∠MOD与∠AON的度数.
∠FOM,求∠MOD与∠AON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,等边三角形![]() 沿射线
沿射线![]() 向右平移到
向右平移到![]() 的位置,连接
的位置,连接![]() 、
、![]() ,则下列结论:(1)
,则下列结论:(1)![]() (2)
(2)![]() 与
与![]() 互相平分(3)四边形
互相平分(3)四边形![]() 是菱形(4)
是菱形(4)![]() ,其中正确的个数是( )
,其中正确的个数是( )
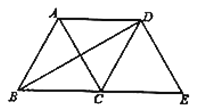
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,把△ABC折叠,使点B与点A重合,折痕交AB于点M,交BC于点N.如果△CAN是等腰三角形,则∠B的度数为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com