
【题目】如图所示,等边三角形![]() 沿射线
沿射线![]() 向右平移到
向右平移到![]() 的位置,连接
的位置,连接![]() 、
、![]() ,则下列结论:(1)
,则下列结论:(1)![]() (2)
(2)![]() 与
与![]() 互相平分(3)四边形
互相平分(3)四边形![]() 是菱形(4)
是菱形(4)![]() ,其中正确的个数是( )
,其中正确的个数是( )
A. 1B. 2C. 3D. 4
【答案】D
【解析】
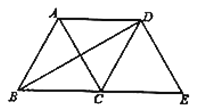
先求出∠ACD=60°,继而可判断△ACD是等边三角形,从而可判断①是正确的;根据①的结论,可判断四边形ABCD是平行四边形,从而可判断②是正确的;再结合①的结论,可判断③正确;根据菱形的对角线互相垂直可得AC⊥BD,再根据平移后对应线段互相平行可得∠BDE=∠COD=90°,进而判断④正确.
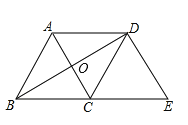
解:如图:∵△ABC,△DCE是等边三角形
∴∠ACB=∠DCE=60°,AC=CD
∴∠ACD=180°-∠ACB-∠DCE=60°
∴△ACD是等边三角形
∴AD=AC=BC,故①正确;
由①可得AD=BC
∵AB=CD
∴四边形ABCD是平行四边形,
∴BD、AC互相平分,故②正确;
由①可得AD=AC=CE=DE故四边形ACED是菱形,即③ 正确
∵四边形ABCD是平行四边形,BA=BC
∴.四边形ABCD是菱形
∴AC⊥BD,AC//DE
∴∠BDE=∠COD=90°
∴BD⊥DE,故④正确
综上可得①②③④正确,共4个.
故选:D


科目:初中数学 来源: 题型:
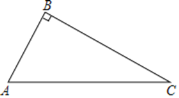
【题目】如图,在△ABC中,∠ABC=90°,
(1)按下列要求完成尺规作图:作线段AC的垂直平分线l,交AC于点O;连接BO并延长至D,使得OD=OB;连接DA、DC(保留作图痕迹,请标明字母);
(2)判断四边形ABCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
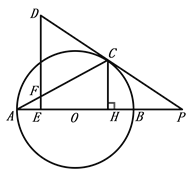
【题目】如图,AB为⊙O直径,过⊙O外的点D作DE⊥OA于点E,射线DC切⊙O于点C、交AB的延长线于点P,连接AC交DE于点F,作CH⊥AB于点H.
(1)求证:∠D=2∠A;
(2)若HB=2,cosD=![]() ,请求出⊙O的半径长.
,请求出⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,∠C=90°.
(1)如图1,在边BC上求作点P,使得点P到AB的距离等于点P到点C的距离.(尺规作图,保留痕迹)
(2)如图2,请利用没有刻度的直尺和圆规在线段AB上找一点F,使得点F到AC的距离等于FB(注:不写作法,保留痕迹,对图中涉及到点用字母进行标注)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子
产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:
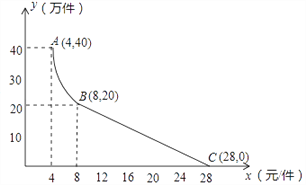
每年的年销售量![]() (万件)与销售价格
(万件)与销售价格![]() (元/件)的关系如图所示,其中AB为反比例函数图象的一
(元/件)的关系如图所示,其中AB为反比例函数图象的一
部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为![]() (万元).(注:若上一
(万元).(注:若上一
年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出![]() (万件)与
(万件)与![]() (元/件)之间的函数关系式;
(元/件)之间的函数关系式;
(2)求出第一年这种电子产品的年利润![]() (万元)与
(万元)与![]() (元/件)之间的函数关系式,并求出第一年年利润的最大值;
(元/件)之间的函数关系式,并求出第一年年利润的最大值;
(3)假设公司的这种电子产品第一年恰好按年利润![]() (万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格
(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格![]() (元)定在8元以上(
(元)定在8元以上(![]() ),当第二年的年利润不低于103万元时,请结合年利润
),当第二年的年利润不低于103万元时,请结合年利润![]() (万元)与销售价格
(万元)与销售价格![]() (元/件)的函数示意图,求销售价格
(元/件)的函数示意图,求销售价格![]() (元/件)的取值范围.
(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中AD=12,AB=9,E为AD的中点,G是DC上一点,连接BE,BG,GE,并延长GE交BA的延长线于点F,GC=5
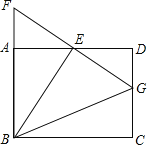
(1)求BG的长度;
(2)求证:![]() 是直角三角形
是直角三角形
(3)求证:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com