
【题目】已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F。

(1)图中哪条线段和BE相等?为什么?
(2)若AB=6,AC=3,求BE的长。
【答案】(1)BE=CF,理由见解析;(2)![]()
【解析】
(1)连CD、BD,如图,根据角平行线的性质定理得到DE=CF,根据线段垂直平分线的性质得CD=BD,则可利用“HL“证明Rt△CDF≌Rt△BDE,从而得到BE=CF;
(2)先证明Rt△ADF≌Rt△ADE得到AE=AF,设BE=CF=x,则AE=6-x,而AE=AF=AC+CF=3+x,则3+x=6-x,然后解方程求出x即可.
(1)BE=CF.理由如下:
连CD、BD,如图,
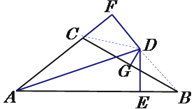
∵AD平分∠BAE,DE⊥AB,DF⊥AC,
∴DE=CF,
又∵DG垂直平分BC,
∴CD=BD,
在Rt△CDF和Rt△BDE中
![]() ,
,
∴Rt△CDF≌Rt△BDE(HL),
∴BE=CF;
(2)在Rt△ADF和Rt△ADE中,
∴Rt△ADF≌Rt△ADE(HL),
∴AE=AF,
设BE=CF=x,则AE=6-x,
∵AF=AC+CF=3+x,
∴3+x=6-x,解得x=![]() ,
,
即BE=![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
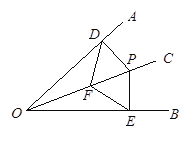
【题目】如图,OC是∠AOB的角平分线,P是OC上一点.PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外研究小组为了解学生参加课外体育活动的情况,采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名同学的兴趣爱好![]() 每人只能选其中一项
每人只能选其中一项![]() ,并将调查结果绘制成统计图,请根据图中提供的信息解答下列问题:
,并将调查结果绘制成统计图,请根据图中提供的信息解答下列问题:
![]() 在这次考察中一共调查了______名学生,请补全条形统计图;
在这次考察中一共调查了______名学生,请补全条形统计图;
![]() 被调查同学中恰好有4名学来自初一2班,其中有2名同学选择了篮球,有2名同学选择了乒乓球,曹老师打算从这4名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好都选择同一种球的概率.
被调查同学中恰好有4名学来自初一2班,其中有2名同学选择了篮球,有2名同学选择了乒乓球,曹老师打算从这4名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好都选择同一种球的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
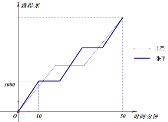
【题目】“绿带城中挂,人在画中游”,张平和王亮同学周末相约骑行于“步移景异,心旷神怡”的温江田园绿道,他们从同一地方同时骑自行车出发(骑行过程中速度保持不变),最后同时到达了同一个地方. 如图刻画了他们离出发点的路程(单位:米)与出发后的时间(单位:分钟)之间的关系. 已知张平中途两次休息时间相同,三段骑行时间也分别相同;王亮中途休息一次,两段骑行时间相同. 张平总的休息时间比王亮的休息时间多![]() 分钟. 请结合图中信息解答下列问题:
分钟. 请结合图中信息解答下列问题:
(1)在这次骑行活动中,他们的骑行路程都是多少米?
(2)求出张平和王亮的骑行速度分别是多少米/分钟?
(3)求出王亮出发后第一次追上张平的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() 下列结论中:
下列结论中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有两个不相等的实数根;
有两个不相等的实数根;![]() 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为![]() ;
;![]() 若点
若点![]() 在该抛物线上,则
在该抛物线上,则![]() .
.
其中正确的有![]()
![]()

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM平分∠AEF交CD于点M,且∠FEM=∠FME.

(1)直线AB与直线CD是否平行,说明你的理由;
(2)如图2,点G是射线MD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.
①当点G在点F的右侧时,若β=60°,求α的度数;
②当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备租用一批汽车,现有甲、乙两种客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人.已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.求1辆甲种客车和1辆乙种客车的租金分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
①请画出△ABC关于y轴对称的△A1B1C1;
②请画出△ABC关于x轴对称的△A2B2C2的各点坐标;
③在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com