
【题目】学校准备租用一批汽车,现有甲、乙两种客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人.已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.求1辆甲种客车和1辆乙种客车的租金分别是多少元?
科目:初中数学 来源: 题型:
【题目】对于实数a,b,我们可以用min{a,b}表示a,b两数中较小的数,例如min{3,-1}=-1,min{2,2}=2. 类似地,若函数y1、y2都是x的函数,则y=min{y1, y2}表示函数y1和y2的“取小函数”.
(1)设y1=x,y2=![]() ,则函数y=min{x,
,则函数y=min{x, ![]() }的图像应该是 中的实线部分.
}的图像应该是 中的实线部分.

(2)请在下图中用粗实线描出函数y=min{(x-2)2, (x+2)2}的图像,并写出该图像的三条不同性质:

① ;
② ;
③ ;
(3)函数y=min{(x-4)2, (x+2)2}的图像关于 对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内:
﹣5,|-![]() |,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
|,﹣12,0,﹣3.14,+1.99,﹣(﹣6),![]()
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A(6,0),C(0,4)点D与坐标原点O重合,动点P从点O出发,以每秒2个单位的速度沿O﹣A﹣B﹣C的路线向终点C运动,连接OP、CP,设点P运动的时间为t秒,△CPO的面积为S,下列图象能表示t与S之间函数关系的是( )

A.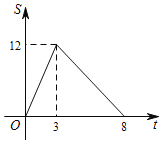
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有A、B两个阅览室,甲、乙、丙三名学生各自随机选择其中的一个阅览室阅读.
(1)下列事件中,是必然事件的为( )
A.甲、乙同学都在A阅览室 B.甲、乙、丙同学中至少两人在A阅览室
C.甲、乙同学在同一阅览室 D.甲、乙、丙同学中至少两人在同一阅览室
(2)用画树状图的方法求甲、乙、丙三名学生在同一阅览室阅读的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,△ABC的三个顶点分别是A(﹣2,﹣2)、B(﹣4,﹣1)、C(﹣4,﹣4).
(Ⅰ)画出△ABC关于原点O或中心对称的△A1B1C1;
(Ⅱ)作出点A关于x轴的对称点A′,若把点A′向右平移a个单位长度后落在△A1B1C1的内部(不包括顶点和边).
①在图中画出点A′,并写出点A′坐标 .
②写出a的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com