
【题目】已知![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() .点
.点![]() 在
在![]() 上(
上(![]() 点与
点与![]() 三点不重合).连接
三点不重合).连接![]() .请你根据题意画出图形并用等式直接写出
.请你根据题意画出图形并用等式直接写出![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3

(1)求证:BN=DN;
(2)求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(方法回顾)证明:三角形中位线定理.
已知:如图1,![]() 中,D、E分别是AB、AC的中点.
中,D、E分别是AB、AC的中点.
求证:![]() ,
,![]() .
.
证明:如图1,延长DE到点F,使得![]() ,连接CF;
,连接CF;
请继续完成证明过程;

(2)(问题解决)
如图2,在矩形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若![]() ,
,![]() ,
,![]() ,求GF的长.
,求GF的长.
(3)(思维拓展)
如图3,在梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AD的中点,G、F分别为AB、CD边上的点,若
,E为AD的中点,G、F分别为AB、CD边上的点,若![]() ,
,![]() ,
,![]() ,求GF的长.
,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 两点,其中点
两点,其中点![]() 的横坐标是
的横坐标是![]() .
.
⑴求这条直线的函数关系式及点![]() 的坐标 ;
的坐标 ;
⑵在![]() 轴上是否存在点
轴上是否存在点![]() ,使得△
,使得△![]() 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
⑶过线段![]() 上一点
上一点![]() ,作
,作![]() ∥
∥![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 在第一象限;点
在第一象限;点![]() ,当点
,当点![]() 的横坐标为何值时,
的横坐标为何值时, ![]() 的长度最大?最大值是多少?
的长度最大?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
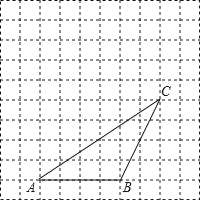
【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点(网格线的交点)上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′;
(3)若连接BB′,CC′,则这两条线段的关系是_______;
(4)△ABC的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() .把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是__________.
.把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备租用一批汽车,现有甲、乙两种客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人.已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.求1辆甲种客车和1辆乙种客车的租金分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国庆”期间,某电影院装修后重新开业,试营业期间统计发现,影院每天售出的电影票张数y(张)与电影票售价![]() (元/张)之间满足一次函数关系:
(元/张)之间满足一次函数关系: ![]() ,
, ![]() 是整数,影院每天运营成本为1600元,设影院每天的利润为w(元)(利润=票房收入
是整数,影院每天运营成本为1600元,设影院每天的利润为w(元)(利润=票房收入![]() 运营成本).
运营成本).
(1)试求w与![]() 之间的函数关系式;
之间的函数关系式;
(2)影院将电影票售价定为多少时,每天获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com