【题目】如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC=2,求∠BPC的度数.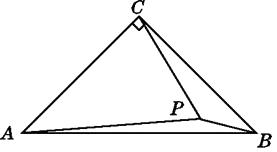
【答案】解:如图,将△CPB绕点C顺时针旋转90°,得△CP'A,
则P'C=PC=2,P'A=PB=1. ∠PCP'=90°, ∠BPC=∠AP'C ，
∴∠CP'P=45° ；
连接PP',
∴PP'2=22+22=8.
又P'A=1,PA=3,而PP'2+P'A2=8+1=9,PA2=9,
∴PP'2+P'A2=PA2.
∴∠AP'P=90°.
又∠CP'P=45°,
∴∠BPC=∠CP'A=135°.
【解析】如图,将△CPB绕点C顺时针旋转90°,得△CP'A,根据旋转的性质知, P'C=PC=2,P'A=PB=1， ∠PCP'=90°, ∠BPC=∠AP'C ，根据等腰直角三角形的性质得出∠CP'P=45° ， 连接PP',根据勾股定理得出PP'2=22+22=8. 根据勾股定理的逆定理PP'2+P'A2=PA2 ， 从而得出∠AP'P=90°,根据角的和差及等量代换得出∠BPC=∠CP'A=135°.
科目：初中数学 来源： 题型：
【题目】如图，点A，B的坐标分别为（1， 4）和（4， 4），抛物线
的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为
，则点D的横坐标最大值为_______。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在坡顶
处的同一水平面上有一座古塔
，数学兴趣小组的同学在斜坡底
处测得该塔的塔顶
的仰角为
，然后他们沿着坡度为
的斜坡
攀行了
米，在坡顶
处又测得该塔的塔顶
的仰角为
．求古塔
的高度．（结果精确到
米，参考数据： 
， 
， 
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中，直线y1=2x﹣2与坐标轴交于A、B两点，与双曲线y2=
（x＞0）交于点C，过点D作CD⊥x轴，垂足为D，且OA=AD，则以下结论：
①S△ADB=S△ADC；②当0＜x＜3时，y1＜y2；③如图，当x=3时，EF=
；④方程2x2﹣2x﹣k=0有解．
其中正确结论的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】温家宝总理强调，“十二五”期间，将新建保障性住房36000000套，用于解决中低收入和新参加工作的大学生住房的需求．把36000000用科学记数法表示应是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,△ABC在平面直角坐标系中.
（1）若把△ABC向上平移2个单位长度,再向左平移1个单位长度得到△A1B1C1,写出A1,B1,C1的坐标;
（2）求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
