
【题目】如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求:
(1)AB的长;
(2)四边形ABCD的面积.
【答案】
(1)解:如图,延长AD,BC交于点E.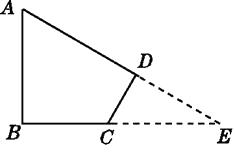
在Rt△ABE中,∠A=60°,
∴∠E=30°.
在Rt△CDE中,CD=4,∠E=30°.
∴CE=2CD=8.
∴BE=BC+CE=6+8=14.
设AB=x,则AE=2x,
根据勾股定理得:x2+142=(2x)2,
解得x= ![]() ,
,
则AB= ![]() 。
。
(2)解:在Rt△CDE中,∠CDE=90°,
∴DE= ![]() =
= ![]() =4
=4 ![]() .
.
∴S四边形ABCD=S△ABE-S△CDE= ![]() ·AB·BE-
·AB·BE- ![]() ·CD·DE=
·CD·DE= ![]() ×
× ![]() ×14-
×14- ![]() ×4×4
×4×4 ![]() =
= ![]() .
.
【解析】(1)如图,延长AD,BC交于点E,根据三角形的内角和得出∠E=30°,根据含30°角的直角三角形的边之间的关系得出CE=2CD=8 ,根据线段的和差得出BE=BC+CE=6+8=14,设AB=x,根据含30°角的直角三角形的边之间的关系则AE=2x,根据勾股定理得:x2+142=(2x)2 ,解方程求出x的值,即得到AB的长度;
(2)根据勾股定理得出DE的长,然后根据S四边形ABCD=S△ABE-S△CDE计算出答案。
【考点精析】掌握三角形的面积和含30度角的直角三角形是解答本题的根本,需要知道三角形的面积=1/2×底×高;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】下列选项中,可以用来说明命题“两个锐角的和是锐角”是假命题的反例的是( )
A.∠A=30°,∠B=40°
B.∠A=30°,∠B=110°
C.∠A=30°,∠B=70°
D.∠A=30°,∠B=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某油箱容量为60 L的汽车,加满汽油后行驶了100 Km时,油箱中的汽油大约消耗了![]() ,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
A. y=0.12x,x>0 B. y=60﹣0.12x,x>0 C. y=0.12x,0≤x≤500 D. y=60﹣0.12x,0≤x≤500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知实数a、b满足(a+b)2=3,(a﹣b)2=27,求a2+b2的值.
(2)先化简,再求值:3a(2a2﹣4a+3)﹣2a2(3a+4),其中a=﹣2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com