
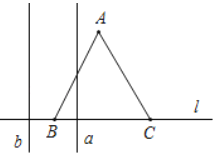
【题目】如图,边长为![]() 的正
的正![]() 的边
的边![]() 在直线
在直线![]() 上,两条距离为
上,两条距离为![]() 的平行直线
的平行直线![]() 和
和![]() 垂直于直线
垂直于直线![]() ,
,![]() 和
和![]() 同时向右移动(
同时向右移动(![]() 的起始位置在
的起始位置在![]() 点),速度均为每秒
点),速度均为每秒![]() 个单位,运动时间为
个单位,运动时间为![]() (秒),直到
(秒),直到![]() 到达
到达![]() 点停止,在
点停止,在![]() 和
和![]() 向右移动的过程中,记
向右移动的过程中,记![]() 夹在
夹在![]() 和
和![]() 间的部分的面积为
间的部分的面积为![]() ,则
,则![]() 关于
关于![]() 的函数图象大致为( )
的函数图象大致为( )
A.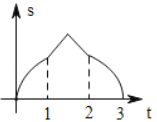 B.
B.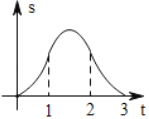
C.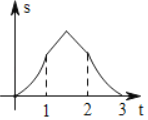 D.
D.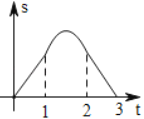
【答案】B
【解析】
依据a和b同时向右移动,分三种情况讨论,求得函数解析式,进而得到当0≤t<1时,函数图象为开口向上的抛物线的一部分,当1≤t<2时,函数图象为开口向下的抛物线的一部分,当2≤t≤3时,函数图象为开口向上的抛物线的一部分.
如图①,当0≤t<1时,BE=t,DE=![]() t,
t,
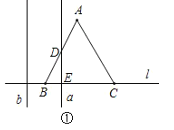
∴s=S△BDE=![]() ×t×
×t×![]() t=
t=![]() t2;
t2;
如图②,当1≤t<2时,CE=2t,BG=t1,

∴DE=![]() (2t),FG=
(2t),FG=![]() (t1),
(t1),
∴s=S五边形AFGED=S△ABCS△BGFS△CDE
=![]() ×2×
×2×![]()
![]() ×(t1)×
×(t1)×![]() (t1)
(t1)![]() ×(2t)×
×(2t)×![]() (2t)
(2t)
=![]() t2+3
t2+3![]() t
t![]() ;
;
如图③,当2≤t≤3时,CG=3t,GF=![]() (3t),
(3t),
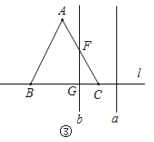
∴s=S△CFG=![]() ×(3t)×
×(3t)×![]() (3t)=
(3t)=![]() t23
t23![]() t+
t+![]() ,
,
综上所述,当0≤t<1时,函数图象为开口向上的抛物线的一部分;当1≤t<2时,函数图象为开口向下的抛物线的一部分;当2≤t≤3时,函数图象为开口向上的抛物线的一部分,
故选B.


科目:初中数学 来源: 题型:
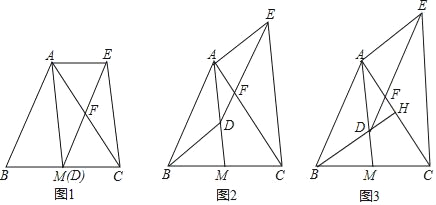
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM.
①求∠CAM的度数;
②当FH=![]() ,DM=4时,求DH的长.
,DM=4时,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
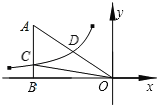
【题目】如图,已知双曲线![]() (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为_____.
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“创科集团”会议室内的一个长为6米、宽为4米的矩形ABCD墙面需要进行装饰,设计图案如图所示,将矩形ABCD墙面分割成3个区域,中间“十”字形区域甲的宽度均为1米,四个角为四个全等的直角三角形,△AEF,△BGH,△CMN,△DPQ为区域乙,剩下部分为区域丙,其中AE=BG=CN=DP,设EG=HM=NP=FQ=x(米)(1≤x≤3)
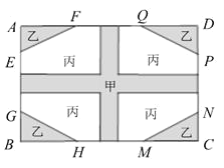
(1)当x=2时,求区域乙的面积;
(2)求区域丙的面积的最大值;
(3)为了图案富有美感,设置区域乙与区域丙的面积之比为1:4,在区域甲、区域乙、区域丙分别嵌贴甲、乙、丙三种不同的装饰板,这三种装饰板每平方米的单价分别为a(百元),b(百元),c(百元)(a,b,c均为整数,且6<a<10),若a+b+c=20,整个墙面嵌贴共花费了150(百元),求三种装饰板每平方米的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到![]() 、
、![]() 两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往
两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往![]() 、
、![]() 两城镇的运费分别为每辆800元和900元,用小货车运往
两城镇的运费分别为每辆800元和900元,用小货车运往![]() 、
、![]() 两城镇的运费分别为每辆400元和600元.
两城镇的运费分别为每辆400元和600元.
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往![]() 城镇,其余货车前往
城镇,其余货车前往![]() 城镇,设前往
城镇,设前往![]() 城镇的大货车为
城镇的大货车为![]() 辆,前往
辆,前往![]() 、
、![]() 两城镇总费用为
两城镇总费用为![]() 元,试求出
元,试求出![]() 与
与![]() 的函数解析式.若运往
的函数解析式.若运往![]() 城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
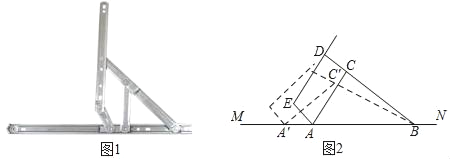
【题目】“滑块铰链”是一种用于连接窗扇和窗框,使窗户能够开启和关闭的连杆式活动链接装置(如图1).图2是“滑块铰链”的平面示意图,滑轨MN安装在窗框上,悬臂DE安装在窗扇上,支点B、C、D始终在一条直线上,已知托臂AC=20厘米,托臂BD=40厘米,支点C,D之间的距离是10厘米,张角∠CAB=60°.
(1)求支点D到滑轨MN的距离(精确到1厘米);
(2)将滑块A向左侧移动到A′,(在移动过程中,托臂长度不变,即AC=A′C′,BC=BC′)当张角∠C′A'B=45°时,求滑块A向左侧移动的距离(精确到1厘米).(备用数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45,
≈2.45,![]() ≈2.65)
≈2.65)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴交于点A,与y轴交于点C,矩形ACBE的顶点B在第一象限的反比例函数
轴交于点A,与y轴交于点C,矩形ACBE的顶点B在第一象限的反比例函数![]() 图像上,过点B作
图像上,过点B作![]()
![]() ,垂足为F,设OF=t.
,垂足为F,设OF=t.
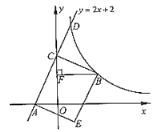
(1)求∠ACO的正切值;
(2)求点B的坐标(用含t的式子表示);
(3)已知直线![]() 与反比例函数
与反比例函数![]() 图像都经过第一象限的点D,联结DE,如果
图像都经过第一象限的点D,联结DE,如果![]() 轴,求m的值.
轴,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
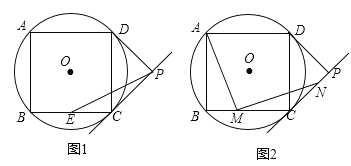
【题目】如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com