Question

【题目】如图，△ABC是等腰直角三角形，∠A=90°，点P、Q分别是AB、AC上的一动点，且满足BP=AQ，D是BC的中点．

（1）求证：△PDQ是等腰直角三角形；
（2）当点P运动到什么位置时，四边形APDQ是正方形，并说明理由．

Answer 1

【答案】
（1）证明：连接AD

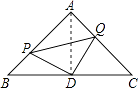
∵△ABC是等腰直角三角形，D是BC的中点

∴AD⊥BC，AD=BD=DC，∠DAQ=∠B，

在△BPD和△AQD中，

，

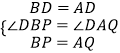∴△BPD≌△AQD（SAS），

∴PD=QD，∠ADQ=∠BDP，

∵∠BDP+∠ADP=90°

∴∠ADP+∠ADQ=90°，即∠PDQ=90°，

∴△PDQ为等腰直角三角形

（2）解：当P点运动到AB的中点时，四边形APDQ是正方形；理由如下：

∵∠BAC=90°，AB=AC，D为BC中点，

∴AD⊥BC，AD=BD=DC，∠B=∠C=45°，

∴△ABD是等腰直角三角形，

当P为AB的中点时，DP⊥AB，即∠APD=90°，

又∵∠A=90°，∠PDQ=90°，

∴四边形APDQ为矩形，

又∵DP=AP= AB，

∴矩形APDQ为正方形（邻边相等的矩形为正方形）．

【解析】（1）连接AD，根据直角三角形的性质可得AD=BD=DC，从而证明△BPD≌△AQD，得到PD=QD，∠ADQ=∠BDP，则△PDQ是等腰三角形；由∠BDP+∠ADP=90°，得出∠ADP+∠ADQ=90°，得到△PDQ是直角三角形，从而证出△PDQ是等腰直角三角形；（2）若四边形APDQ是正方形，则DP⊥AP，得到P点是AB的中点．