
【题目】如图所示,直线L1的解析表达式为y=﹣3x+3,且L1与x轴交于点D.直线L2经过点A,B,直线L1 , L2交于点C. 
(1)求直线L2的解析表达式;
(2)求△ADC的面积;
(3)在直线L2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
【答案】
(1)解:设直线L2的解析表达式为y=kx+b,
把A(4,0)、B(3,﹣ ![]() )代入得
)代入得 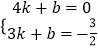 ,解得
,解得 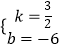 ,
,
所以直线L2的解析表达式为y= ![]() x﹣6
x﹣6
(2)解:解方程组 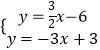 得
得 ![]() ,则C(2,﹣3);
,则C(2,﹣3);
当y=0时,﹣3x+3=0,解得x=1,则D(1,0),
所以△ADC的面积= ![]() ×(4﹣1)×3=
×(4﹣1)×3= ![]()
(3)解:因为点P与点C到AD的距离相等,
所以P点的纵坐标为3,
当y=3时, ![]() x﹣6=3,解得x=6,
x﹣6=3,解得x=6,
所以P点坐标为(6,3)
【解析】(1)利用待定系数法求直线L2的解析表达式;(2)先解方程组 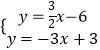 确定C(2,﹣3),再利用x轴上点的坐标特征确定D点坐标,然后根据三角形面积公式求解;(3)由于△ADP与△ADC的面积相等,根据三角形面积公式得到点P与点C到AD的距离相等,则P点的纵坐标为3,对于函数y=
确定C(2,﹣3),再利用x轴上点的坐标特征确定D点坐标,然后根据三角形面积公式求解;(3)由于△ADP与△ADC的面积相等,根据三角形面积公式得到点P与点C到AD的距离相等,则P点的纵坐标为3,对于函数y= ![]() x﹣6,计算出函数值为3所对应的自变量的值即可得到P点坐标.
x﹣6,计算出函数值为3所对应的自变量的值即可得到P点坐标.


科目:初中数学 来源: 题型:
【题目】下列各式变形中,是因式分解的是( )
A.a2﹣2ab+b2﹣1=(a﹣b)2﹣1
B.2x2+2x=2x2(1+ ![]() )
)
C.x4﹣1=(x2+1)(x+1)(x﹣1)
D.(x+2)(x﹣2)=x2﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C,D四支足球队分在同一小组进行单循环足球比赛,争夺出线权,比赛规则规定:胜一场得3分,平一场得1分,负一场得0分,小组中积分最高的两个队(有且只有两个队)出线,小组赛结束后,如果A队没有全胜,那么A队的积分至少要几分才能保证一定出线?请说明理由.
[注:单循环比赛就是小组内的每一个队都要和其他队赛一场].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (2016福建南平第16题)如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,给出下列结论:
①CD=CP=CQ;
②∠PCQ的大小不变;
③△PCQ面积的最小值为![]() ;
;
④当点D在AB的中点时,△PDQ是等边三角形,其中所有正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点. 
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 在同一平面内,过直线外一点向该直线画垂线,垂足一定在该直线上
B. 在同一平面内,过线段或射线外一点向该线段或射线画垂线,垂足一定在该线段或射线上
C. 过线段或射线外一点不一定能画出该线段或射线的垂线
D. 过直线外一点与直线上一点画的一条直线与该直线垂直
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com