
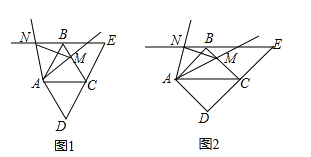
����Ŀ�� ��2016����Ӫ�ڵ�25�⣩��֪����ͼ�٣�����D=60�������ABCD�ضԽ���AC����������ADC������DC����ƽ�ƣ��õ���BCE����MΪ��BC��һ�㣨��M�����B����C�غϣ���������AM�Ƶ�A��ʱ����ת60�㣬��EB���ӳ��߽��ڵ�N������MN��
��1������֤����ANB=��AMC��
��̽����AMN����״��
��2����ͼ�ڣ�������ABCD��Ϊ������ABCD��������AM�Ƶ�A��ʱ����ת45�㣬ԭ�������������䣬��1���еĢ١������������Ƿ���Ȼ����������������ֱ��д�����ۣ�������������д���仯��Ľ��۲�֤����

���𰸡���1����֤�����������ڡ�AMN�ǵȱ�����������2���ٳ������ڲ���������AMN�ǵ���ֱ�������Σ�
��������
�����������1�����������ο�֪�ı���ȣ�������D=60��õȱ���ADC�͵ȱ���ABC����Խ���AC���ı߶���ȣ�����ASA֤����ANB�ա�AMC���ý��ۣ�
�ڸ�����һ������60��ĵ����������ǵȱ������εó�����AMN�ǵȱ������Σ�
��2���ٳ��������������ε�45��Ǻ�����AM�Ƶ�A��ʱ����ת45�㣬֤����ANB�ס�AMC������ANB=��AMC��
�ڲ���������AMN�ǵ���ֱ�������Σ����â��е���ANB�ס�AMC���ñ���ʽ���б��κ���֤����NAM�ס�BAD������AMN�ǵ���ֱ�������Σ�
�����������1����ͼ1�������ı���ABCD�����Σ���AB=BC=CD=AD���ߡ�D=60�㣬���ADC����ABC�ǵȱ������Σ���AB=AC����BAC=60�㣬�ߡ�NAM=60�㣬���NAB=��CAM������ADC������DC����ƽ�Ƶõ���BCE����֪��CBE=60�㣬�ߡ�ABC=60�㣬���ABN=60�㣬���ABN=��ACB=60�㣬���ANB�ա�AMC�����ANB=��AMC��
����ͼ1����AMN�ǵȱ������Σ������ǣ�
����ANB�ա�AMC����AM=AN���ߡ�NAM=60�㣬���AMN�ǵȱ������Σ�
��2������ͼ2����ANB=��AMC�����������ǣ�
��������ABCD�У����BAC=��DAC=��BCA=45�㣬�ߡ�NAM=45�㣬���NAB=��MAC����ƽ�Ƶã���EBC=��CAD=45�㣬�ߡ�ABC=90�㣬���ABN=180�㩁90�㩁45��=45�㣬���ABN=��ACM=45�㣬���ANB�ס�AMC�����ANB=��AMC��
����ͼ2������������AMN�ǵ���ֱ�������Σ������ǣ�
�ߡ�ANB�ס�AMC����![]() ����
����![]() ���ߡ�NAM=��BAC=45�㣬���NAM�ס�BAC�����ANM=��ABC=90�㣬���AMN�ǵ���ֱ�������Σ�
���ߡ�NAM=��BAC=45�㣬���NAM�ס�BAC�����ANM=��ABC=90�㣬���AMN�ǵ���ֱ�������Σ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���һ����11000Ԫ����ij��ƴװ�����˽������ۣ��ܿ�����һ�գ��̼�����24000Ԫ�ڶ��ι���ͬ������ˣ������������ǵ�һ�ε�2���������۹���10Ԫ��
��1������̼ҵ�һ�ι��������˶��ٸ���
��2�������л����˶�����ͬ�ı�����ۣ�Ҫ��ȫ��������ϵ������ʲ�����20%���������������أ�����ôÿ�������˵ı�������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��x+10��x�ᡢy��ֱ��ڵ�B��C����A������Ϊ��8��0����P��x��y����ֱ��y=��x+10�ڵ�һ������һ�����㣮 
��1�����OPA�����S��x�ĺ�����ϵʽ����д���Ա�����x��ȡֵ��Χ��
��2������OPA�����Ϊ10ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��2016������ƽ��16�⣩��ͼ��������ABC�У�CA=CB=4����ACB=120�㣬��D���߶�AB���˶�������A��B�غϣ�������CAD����CBD�ֱ���ֱ��CA��CB���۵õ���CAP����CBQ���������н��ۣ�
��CD=CP=CQ��
����PCQ�Ĵ�С���䣻
����PCQ�������СֵΪ![]() ��
��
�ܵ���D��AB���е�ʱ����PDQ�ǵȱ������Σ�����������ȷ���۵������ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ���A=90�㣬��P��Q�ֱ���AB��AC�ϵ�һ���㣬������BP=AQ��D��BC���е㣮 
��1����֤����PDQ�ǵ���ֱ�������Σ�
��2������P�˶���ʲôλ��ʱ���ı���APDQ�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x=1�ǹ���x��һԪ���η���x2+3x��m=0��һ��������m��ֵ�ͷ��̵���һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A����1��5����B����1��0����C����4��3���� 
��1�������ABC�������
��2����ͼ��������ABC����y��ĶԳ�ͼ�Ρ�A1B1C1��
��3��д����A1 �� B1 �� C1�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������3a2��3ab+6a��һ�߳�Ϊ3a�������ܳ��� ��
A.2a��b+2
B.8a��2b
C.8a��2b+4
D.4a��b+2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com