
分析 ①先化简,再计算加减法;
②将除法变为乘法,再约分计算即可求解;
③按照有理数混合运算的顺序,先乘方后乘除最后算加减,有括号的先算括号里面的;
④运用乘法的分配律计算.
解答 解:①-13-(-5)+2
=-13+5+2
=-6;
②$-6×(-1\frac{2}{7})÷\frac{18}{5}$
=6×$\frac{9}{7}$×$\frac{5}{18}$
=$\frac{15}{7}$;
③${({-3})^2}+8×({\frac{1}{2}-\frac{3}{4}})$
=9+8×(-$\frac{1}{4}$)
=9-2
=7;
④$89\frac{24}{25}×(-5)$
=(90-$\frac{1}{25}$)×(-5)
=90×(-5)-$\frac{1}{25}$×(-5)
=-450+$\frac{1}{5}$
=$-449\frac{4}{5}$
点评 本题考查的是有理数的运算能力.注意:
(1)要正确掌握运算顺序,在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序;
(2)去括号法则:--得+,-+得-,++得+,+-得-.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| n | 2 | 3 | 4 | 5 | … |
| a | 22-1 | 32-1 | 42-1 | 52-1 | … |
| b | 4 | 6 | 8 | 10 | … |
| c | 22+1 | 32+1 | 42+1 | 52+1 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
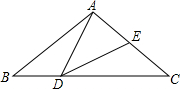 如图,在△ABC中,AB=AC=2,点D在线段BC上运动(点D不与B、C重合),∠B=40°,连结AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,点D在线段BC上运动(点D不与B、C重合),∠B=40°,连结AD,作∠ADE=40°,DE交线段AC于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com