
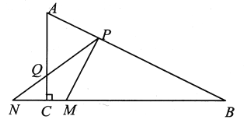
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() ,
,![]() 同时从点
同时从点![]() 出发,分别沿射线
出发,分别沿射线![]() ,
,![]() 方向运动,且满足
方向运动,且满足![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,
,![]() 与直线
与直线![]() 交于点
交于点![]() .设
.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 之间的函数图象大致是( )
之间的函数图象大致是( )
A. 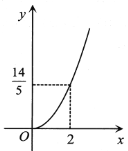 B.
B. 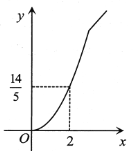 C.
C. 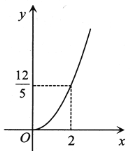
【答案】C
【解析】
先由AQ=PQ,∠ACB=90°及PM⊥AB,推出∠B=∠MPN,再结合∠PNM=∠PNB,证出△PNM∽△BNP,推出线段的比例关系,然后用tanB的值计算出相似比,从而求得当x=2时,点N与点C重合,从而解出PM、PB,进而算出△PMN的面积,从而得解.
∵AQ=PQ,
∴∠A=∠APQ,
∵在Rt△ACB中,∠ACB=90°,
∴∠B+∠A=90°,
∴∠APQ+∠B=90°,
又∵PM⊥AB,
∴∠MPN+∠APQ=90°,
∴∠B=∠MPN,
又∵∠PNM=∠PNB,
∴△PNM∽△BNP,
∴![]() ,
,
∵MN=x,△PMN的面积为y,在Rt△ACB中,∠ACB=90°,AC=4,BC=8,
∴Rt△ACB和Rt△BPM中,tanB=![]() ,
,
∴![]() ,
,
∴当x=2时,PN=4,BN=8,
又∵BC=8,
∴当x=2时,点N与点C重合.
∴BM=BC-MN=8-2=6,
∴在Rt△BPM中,设PM=m,则PB=2m,由勾股定理得:m2+(2m)2=62,
解得m=![]() ,2m=
,2m=![]() ,
,
∴S△PBM=![]() ×
×![]() ÷2=
÷2=![]() ,
,
∵![]() ,
,
∴△PMN的面积y=![]() ×
×![]() =
=![]() ,
,
∴当x=2时,y=![]() ,
,
由选项的图象得,只有C符合要求.
故选C.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
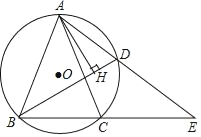
【题目】如图,△ABC内接于⊙O,BC=2,AB=AC,点D为![]() 上的动点,且cos∠ABC=
上的动点,且cos∠ABC=![]() .
.
(1)求AB的长度;
(2)在点D的运动过程中,弦AD的延长线交BC延长线于点E,问ADAE的值是否变化?若不变,请求出ADAE的值;若变化,请说明理由;
(3)在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
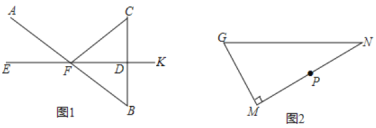
【题目】(1)如图1,已知![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
求证:![]() .
.
(2)如图2,在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点.
的中点.
①用直尺和圆规在![]() 边上求作点
边上求作点![]() ,使得
,使得![]() (保留作图痕迹,不要求写作法);
(保留作图痕迹,不要求写作法);
②在①的条件下,如果![]() ,
,![]() ,P为MN中点,求MQ的长度.
,P为MN中点,求MQ的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,![]() ,
,![]() ,将矩形沿直线EF折叠.使得点A恰好落在BC边上的点G处,且点E、F分别在边AB、AD上(含端点),连接CF.
,将矩形沿直线EF折叠.使得点A恰好落在BC边上的点G处,且点E、F分别在边AB、AD上(含端点),连接CF.
(1)当![]() 时,求AE的长;
时,求AE的长;
(2)当AF取得最小值时,求折痕EF的长;
(3)连接CF,当![]() 是以CG为底的等腰三角形时,直接写出BG的长.
是以CG为底的等腰三角形时,直接写出BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某拦河坝横截面原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°,为了提高拦河坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°,请你计算这个拦河大坝的高度.(参考数据:sin72°≈![]() ,cos72°≈
,cos72°≈![]() ,tan72°
,tan72°![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
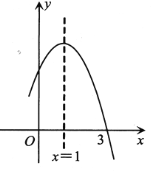
【题目】如图,抛物线![]() 经过点
经过点![]() ,且对称轴为直线
,且对称轴为直线![]() .有四个结论:①
.有四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值.其中正确的结论是( )
时的函数值.其中正确的结论是( )
A. ①②B. ②③C. ①④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的不断提高,旅游已成为人们的一种生活时尚.为 开发新的旅游项目,我市对某山区进行调查,发现一瀑布.为测量它的高度,测 量人员在瀑布的对面山上 D 点处测得瀑布顶端 A 点的仰角是 30°,测得瀑布底端 B 点的俯角是 10°,AB 与水平面垂直.又在瀑布下的水平面测得 CG=27m, GF=17.6m(注:C、G、F 三点在同一直线上,CF⊥AB 于点 F).斜坡 CD=20m, 坡角∠ECD=40°.求瀑布 AB 的高度.(参考数据:![]() ≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 个边长为
个边长为![]() 的相邻正方形的一边均在同一直线上,点
的相邻正方形的一边均在同一直线上,点![]() ,
,![]() ,
,![]() ,…
,…![]() 分别为边
分别为边![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的中点,
的中点,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,…
,…![]() 的面积为
的面积为![]() ,则
,则![]() ________.(用含
________.(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
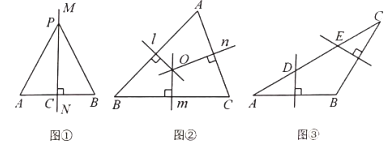
【题目】教材呈现:下图是华师版八年级上册数学教材第94页的部分内容.

请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.
定理应用:
(1)如图②,在![]() 中,直线
中,直线![]() 分别是边AB、BC、AC的垂直平分线.求证:直线
分别是边AB、BC、AC的垂直平分线.求证:直线![]() 交于点
交于点![]() .
.
(2)如图③,在![]() 中,
中,![]() ,边AB的垂直平分线交AC于点D、边BC的垂直平分线交AC于点E.若
,边AB的垂直平分线交AC于点D、边BC的垂直平分线交AC于点E.若![]() ,
,![]() ,则DE的长为___________.
,则DE的长为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com