
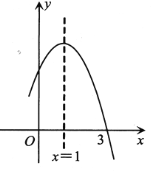
【题目】如图,抛物线![]() 经过点
经过点![]() ,且对称轴为直线
,且对称轴为直线![]() .有四个结论:①
.有四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值.其中正确的结论是( )
时的函数值.其中正确的结论是( )
A. ①②B. ②③C. ①④D. ③④
【答案】D
【解析】
利由抛物线的位置可对①进行判断;利用抛物线与x轴的交点有两个对②进行判断;利用抛物线的对称性得到抛物线与x轴的一个交点坐标为(-1,0),代入解析式则可对③进行判断;由抛物线的对称性和二次函数的性质可对④进行判断.
∵抛物线开口向下,
∴a<0,
∵抛物线交y轴的正半轴,
∴c>0,
∴ac<0,故①错误;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,故②错误;
∵抛物线的对称轴为直线x=1,
而点(3,0)关于直线x=1的对称点的坐标为(-1,0),
∴a-b+c=0,故③正确;
∵抛物线开口向下,对称轴为直线x=1,
∴横坐标是1-m的点的对称点的横坐标为1+m,
∵若m>n>0,
∴1+m>1+n,
∴x=1-m时的函数值小于x=1+n时的函数值,故④正确.
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
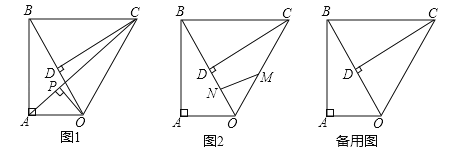
顺时针旋转![]() ,如图1,连接
,如图1,连接![]() .
.
(1)填空:![]()
![]() ;
;
(2)如图1,连接![]() ,作
,作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的长度;
的长度;
(3)如图2,点![]() ,
,![]() 同时从点
同时从点![]() 出发,在
出发,在![]() 边上运动,
边上运动,![]() 沿
沿![]() 路径匀速运动,
路径匀速运动,![]() 沿
沿![]() 路径匀速运动,当两点相遇时运动停止,已知点
路径匀速运动,当两点相遇时运动停止,已知点![]() 的运动速度为1.5单位
的运动速度为1.5单位![]() 秒,点
秒,点![]() 的运动速度为1单位
的运动速度为1单位![]() 秒,设运动时间为
秒,设运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求当
,求当![]() 为何值时
为何值时![]() 取得最大值?最大值为多少?
取得最大值?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
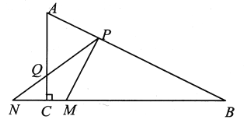
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() ,
,![]() 同时从点
同时从点![]() 出发,分别沿射线
出发,分别沿射线![]() ,
,![]() 方向运动,且满足
方向运动,且满足![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,
,![]() 与直线
与直线![]() 交于点
交于点![]() .设
.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 之间的函数图象大致是( )
之间的函数图象大致是( )
A. 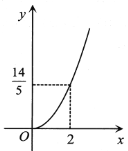 B.
B. 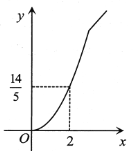 C.
C. 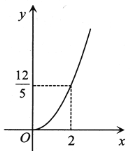
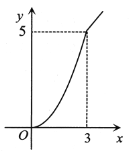
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
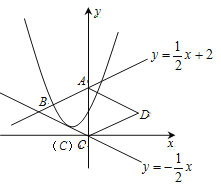
【题目】如图,直线![]() 与y轴交于点A,与直线
与y轴交于点A,与直线![]() 交于点B,以AB为边向右做菱形ABCD,点C恰与原点重合,抛物线
交于点B,以AB为边向右做菱形ABCD,点C恰与原点重合,抛物线![]() 的顶点在直线
的顶点在直线![]() 上移动,若抛物线与菱形的边AB,BC都有公共点,则h的取值范围是( )
上移动,若抛物线与菱形的边AB,BC都有公共点,则h的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
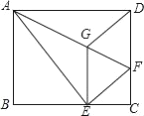
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=![]() GF×AF;
GF×AF;
(3)若![]() ,折痕AF=5
,折痕AF=5![]() cm,则矩形ABCD的周长为 .
cm,则矩形ABCD的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区教育系统为了更好地宣传扫黑除恶专项斗争,印制了应知应会手册,该区教育局想了解教师对扫黑除恶专项斗争应知应会知识掌握程度,抽取了部分教师进行了测试,并将测试成绩绘制成下面两幅统计图,请根据统计图中提供的信息,回答下面问题:
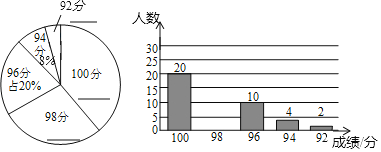
(1)计算样本中,成绩为98分的教师有 人,并补全两个统计图;
(2)样本中,测试成绩的众数是 ,中位数是 ;
(3)若该区共有教师6880名,根据此次成绩估计该区大约有多少名教师已全部掌握扫黑除恶专项斗争应知应会知识?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com