
【题目】一节地理课结束后,小明拿出地球仪,突发奇想:地球仪环形支架的长度比地球仪上画的赤道的长度长多少? 活动一:如图1,求大圆与小圆的周长之差?
活动二:如图2,以O为圆心,任意画出两个圆,两圆半径相差6cm,求大圆与小圆的周长之差?
活动三:若地球仪与环形支架之间的间隙为k(cm),请直接写出地球仪环形支架的长度比地球仪上画的赤道的长度长多少?
【答案】解:活动一:大圆的周长为2×6π=12π,小圆的周长为2×1π=2π, ∴两圆的周长差是12π﹣2π=10π.
活动二:设小圆的半径为r,则大圆的半径为r+6,
∴大圆的周长为2×(r+6)π=12π+2πr,小圆的周长为2×γπ=2πγ,
∴两圆的周长差是12π+2πr﹣2πγ=12π.
活动三:∵地球仪与环形支架之间的间隙为kcm,
∴地球仪环形支架的长度比地球仪上画的赤道的长度长2kπcm
【解析】活动一:根据圆的周长公式求出两圆的周长,做差后即可得出结论; 活动二:设小圆的半径为r,则大圆的半径为r+6,根据圆的周长公式求出两圆的周长,做差后即可得出结论;
活动三:由地球仪与环形支架之间的间隙长度,结合活动一、二得出的结论,代入数据即可得出结论.
【考点精析】关于本题考查的整式加减法则,需要了解整式的运算法则:(1)去括号;(2)合并同类项才能得出正确答案.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】若一个矩形的一边是另一边的两倍,则称这个矩形为方形,如图1,矩形ABCD中,BC=2AB,则称ABCD为方形.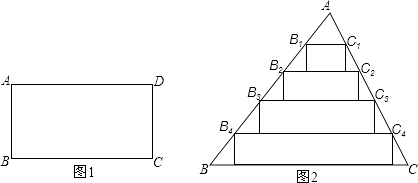
(1)设a,b是方形的一组邻边长,写出a,b的值(一组即可).
(2)在△ABC中,将AB,AC分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使这些矩形的边B1C1 , B2C2 , B3C3 , B4C4的对边分别在B2C2 , B3C3 , B4C4 , BC上,如图2所示.
①若BC=25,BC边上的高为20,判断以B1C1为一边的矩形是不是方形?为什么?
②若以B3C3为一边的矩形为方形,求BC与BC边上的高之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( ) 
A.abc<0
B.2a+b<0
C.a﹣b+c<0
D.4ac﹣b2<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3). 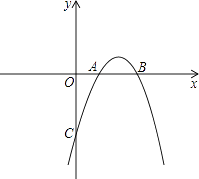
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是反比例函数y= ![]() (k<0)图象上的点,PA垂直x轴于点A(﹣1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=
(k<0)图象上的点,PA垂直x轴于点A(﹣1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB= ![]() .
.
(1)k的值是;
(2)若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x= ![]() . ①求该抛物线的函数解析式;
. ①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某厂生产横截面直径为7cm的圆柱形罐头盒,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头盒侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为( ) 
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.7πcm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内时,∠A与∠1+∠2之间有始终不变的关系是( )

A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2 C. 3∠A=∠1+∠2 D. 3∠A=2(∠1+∠2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com