
【题目】若一个矩形的一边是另一边的两倍,则称这个矩形为方形,如图1,矩形ABCD中,BC=2AB,则称ABCD为方形.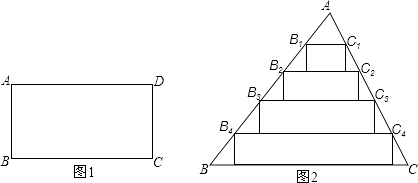
(1)设a,b是方形的一组邻边长,写出a,b的值(一组即可).
(2)在△ABC中,将AB,AC分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使这些矩形的边B1C1 , B2C2 , B3C3 , B4C4的对边分别在B2C2 , B3C3 , B4C4 , BC上,如图2所示.
①若BC=25,BC边上的高为20,判断以B1C1为一边的矩形是不是方形?为什么?
②若以B3C3为一边的矩形为方形,求BC与BC边上的高之比.
【答案】
(1)
解:答案不唯一,如a=2,b=4
(2)
解:①以B1C1为一边的矩形不是方形.
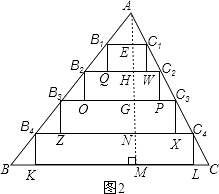
理由是:过A作AM⊥BC于M,交B1C1于E,交B2C2于H,交B3C3于G,交B4C4于N,则AM⊥B4C4,AM⊥B3C3,AM⊥B2C2,AM⊥B1C1,
∵由矩形的性质得:BC∥B1C1∥B2C2∥B3C3∥B4C4,
∴△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,
,
∵AM=20,BC=25,
∴B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,
∴MN=GN=GH=HE=4,
∴B1Q=B2O=B3Z=B4K=4,
即B1C1≠2B1Q,B1Q≠2B1C1,
∴以B1C1为一边的矩形不是方形;
②∵以B3C3为一边的矩形为方形,设AM=h,
∴△ABC∽△AB3C3,
∴ ![]() =
= ![]() ,
,
则AG= ![]() h,
h,
∴MN=GN=GH=HE= ![]() h,
h,
当B3C3=2× ![]() h时,
h时, ![]() =
= ![]() =
= ![]() ;
;
当B3C3= ![]() ×
× ![]() h时,
h时, ![]() =
= ![]() =
= ![]() .
.
综合上述:BC与BC边上的高之比是 ![]() 或
或 ![]() .
.
【解析】(1)答案不唯一,根据已知举出即可;(2)①求出△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4 , 推出 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,求出B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,MN=GN=GH=HE=4,B1Q=B2O=B3Z=B4K=4,根据已知判断即可;
,求出B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,MN=GN=GH=HE=4,B1Q=B2O=B3Z=B4K=4,根据已知判断即可;
②设AM=h,根据△ABC∽△AB3C3 , 得出 ![]() =
= ![]() ,求出MN=GN=GH=HE=
,求出MN=GN=GH=HE= ![]() h,分为两种情况:当B3C3=2×
h,分为两种情况:当B3C3=2× ![]() h时,当B3C3=
h时,当B3C3= ![]() ×
× ![]() h时,代入求出即可.
h时,代入求出即可.


科目:初中数学 来源: 题型:
【题目】如图1,圆规两脚形成的角α称为圆规的张角.一个圆规两脚均为12cm,最大张角150°,你能否画出一个半径为20cm的圆?请借助图2说明理由.(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线l:y=﹣x+2与y轴交于点A,抛物线y=(x﹣1)2+k经过点A,其顶点为B,另一抛物线y=(x﹣h)2+2﹣h(h>1)的顶点为D,两抛物线相交于点C.
(1)求点B的坐标,并说明点D在直线l上的理由;
(2)设交点C的横坐标为m.
交点C的纵坐标可以表示为:或;
(3)如图2,若∠ACD=90°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+4与x轴、y轴分别交于点A、B,点C从点B出发,以每秒5个单位长度的速度向点A匀速运动;同时点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,到达终点后运动立即停止.连接CD,取CD的中点E,过点E作EF⊥CD,与折线DO﹣OA﹣AC交于点F,设运动时间为t秒.
x+4与x轴、y轴分别交于点A、B,点C从点B出发,以每秒5个单位长度的速度向点A匀速运动;同时点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,到达终点后运动立即停止.连接CD,取CD的中点E,过点E作EF⊥CD,与折线DO﹣OA﹣AC交于点F,设运动时间为t秒.
(1)点C的坐标为(用含t的代数式表示);
(2)求证:点E到x轴的距离为定值;
(3)连接DF、CF,当△CDF是以CD为斜边的等腰直角三角形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为准备体育中考,每天早晨坚持锻炼,某天他慢跑到江边,休息一会后快跑回家,能大致反映小明离家的距离y(m)与时间x(s)的函数关系图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒 ![]() 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.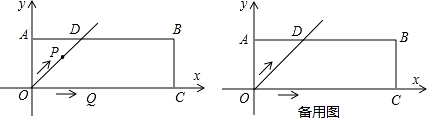
(1)当点P移动到点D时,求出此时t的值;
(2)当t为何值时,△PQB为直角三角形;
(3)已知过O、P、Q三点的抛物线解析式为y=﹣ ![]() (x﹣t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(x﹣t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC,在△ABC外侧作直线CP,点A关于直线CP的对称点为D,连接AD,BD,其中BD交直线CP于点E.
(1)如图1,∠ACP=15°.
①依题意补全图形;
②求∠CBD的度数;
(2)如图2,若45°<∠ACP<90°,直接用等式表示线段AC,DE,BE之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一节地理课结束后,小明拿出地球仪,突发奇想:地球仪环形支架的长度比地球仪上画的赤道的长度长多少? 活动一:如图1,求大圆与小圆的周长之差?
活动二:如图2,以O为圆心,任意画出两个圆,两圆半径相差6cm,求大圆与小圆的周长之差?
活动三:若地球仪与环形支架之间的间隙为k(cm),请直接写出地球仪环形支架的长度比地球仪上画的赤道的长度长多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com