
【题目】在平面直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒 ![]() 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.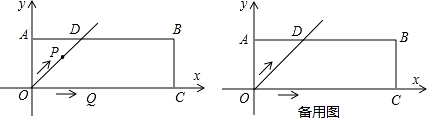
(1)当点P移动到点D时,求出此时t的值;
(2)当t为何值时,△PQB为直角三角形;
(3)已知过O、P、Q三点的抛物线解析式为y=﹣ ![]() (x﹣t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(x﹣t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
【答案】
(1)
解:∵四边形OABC是矩形,
∴∠AOC=∠OAB=90°,
∵OD平分∠AOC,
∴∠AOD=∠DOQ=45°,
∴在Rt△AOD中,∠ADO=45°,
∴AO=AD=2,OD=2 ![]() ,
,
∴t= ![]() =2
=2
(2)
解:要使△PQB为直角三角形,显然只有∠PQB=90°或∠PBQ=90°.
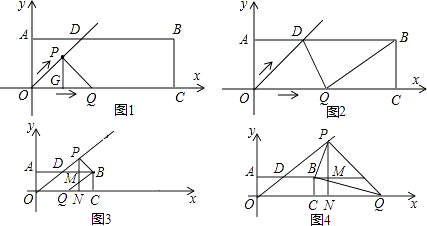
如图1,作PG⊥OC于点G,在Rt△POG中,
∵∠POQ=45°,
∴∠OPG=45°,
∵OP= ![]() t,
t,
∴OG=PG=t,
∴点P(t,t)
又∵Q(2t,0),B(6,2),
根据两点间的距离公式可得:PB2=(6﹣t)2+(2﹣t)2,QB2=(6﹣2t)2+22,PQ2=(2t﹣t)2+t2=2t2,
①若∠PQB=90°,则有PQ2+BQ2=PB2,
即:2t2+[(6﹣2t)2+22]=(6﹣t)2+(2﹣t)2,
整理得:4t2﹣8t=0,
解得:t1=0(舍去),t2=2,
∴t=2,
②若∠PBQ=90°,则有PB2+QB2=PQ2,
∴[(6﹣t)2+(2﹣t)2]+[(6﹣2t)2+22]=2t2,
整理得:t2﹣10t+20=0,
解得:t=5± ![]() .
.
∴当t=2或t=5+ ![]() 或t=5﹣
或t=5﹣ ![]() 时,△PQB为直角三角形.
时,△PQB为直角三角形.
解法2:①如图2,当∠PQB=90°时,
易知∠OPQ=90°,
∴BQ∥OD
∴∠BQC=∠POQ=45°
可得QC=BC=2,
∴OQ=4,
∴2t=4,
∴t=2,
②如图3,当∠PBQ=90°时,若点Q在OC上,
作PN⊥x轴于点N,交AB于点M,
则易证∠PBM=∠CBQ,
∴△PMB∽△QCB
∴ ![]() =
= ![]() ,
,
∴CBPM=QCMB,
∴2(t﹣2)=(2t﹣6)(6﹣t),
化简得t2﹣10t+20=0,
解得:t=5± ![]() ,
,
∴t=5﹣ ![]() ;
;
③如图4,当∠PBQ=90°时,若点Q在OC的延长线上,
作PN⊥x轴于点N,交AB延长线于点M,
则易证∠BPM=∠MBQ=∠BQC,
∴△PMB∽△QCB,
∴ ![]() =
= ![]() ,
,
∴CBPM=QCMB,
∴2(t﹣2)=(2t﹣6)(t﹣6),
化简得t2﹣10t+20=0,
解得:t=5± ![]() ,
,
∴t=5+ ![]()
(3)
解:存在这样的t值,理由如下:
将△PQB绕某点旋转180°,三个对应顶点恰好都落在抛物线上,
则旋转中心为PQ中点,此时四边形PBQB′为平行四边形.
∵PO=PQ,由P(t,t),Q(2t,0),知旋转中心坐标可表示为( ![]() t,
t, ![]() t),
t),
∵点B坐标为(6,2),
∴点B′的坐标为(3t﹣6,t﹣2),
代入y=﹣ ![]() (x﹣t)2+t,得:2t2﹣13t+18=0,
(x﹣t)2+t,得:2t2﹣13t+18=0,
解得:t1= ![]() ,t2=2
,t2=2
【解析】(1)首先根据矩形的性质求出DO的长,进而得出t的值;(2)要使△PQB为直角三角形,显然只有∠PQB=90°或∠PBQ=90°,进而利用勾股定理分别分析得出PB2=(6﹣t)2+(2﹣t)2 , QB2=(6﹣2t)2+22 , PQ2=(2t﹣t)2+t2=2t2 , 再分别就∠PQB=90°和∠PBQ=90°讨论,求出符合题意的t值即可;(3)存在这样的t值,若将△PQB绕某点旋转180°,三个对应顶点恰好都落在抛物线上,则旋转中心为PQ中点,此时四边形PBQB′为平行四边形,根据平行四边形的性质和对称性可求出t的值.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
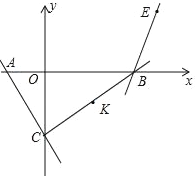
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x﹣
x﹣![]() 交x轴于点A,交y轴于点C,直线y=
交x轴于点A,交y轴于点C,直线y=![]() x﹣5
x﹣5![]() 交x轴于点B,在平面内有一点E,其坐标为(4,
交x轴于点B,在平面内有一点E,其坐标为(4,![]() ),连接CB,点K是线段CB的中点,另有两点M,N,其坐标分别为(a,0),(a+1,0).将K点先向左平移
),连接CB,点K是线段CB的中点,另有两点M,N,其坐标分别为(a,0),(a+1,0).将K点先向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位得K′,当以K′,E,M,N四点为顶点的四边形周长最短时,a的值为_____.
个单位得K′,当以K′,E,M,N四点为顶点的四边形周长最短时,a的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题: 
(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个矩形的一边是另一边的两倍,则称这个矩形为方形,如图1,矩形ABCD中,BC=2AB,则称ABCD为方形.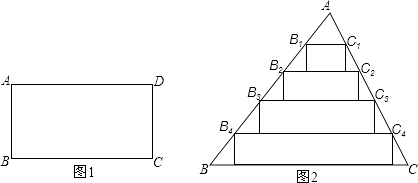
(1)设a,b是方形的一组邻边长,写出a,b的值(一组即可).
(2)在△ABC中,将AB,AC分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使这些矩形的边B1C1 , B2C2 , B3C3 , B4C4的对边分别在B2C2 , B3C3 , B4C4 , BC上,如图2所示.
①若BC=25,BC边上的高为20,判断以B1C1为一边的矩形是不是方形?为什么?
②若以B3C3为一边的矩形为方形,求BC与BC边上的高之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1). ①画出△ABC关于y轴对称的△A1B1C1 , 并写出点C1的坐标;
②连结BC1 , 在坐标平面的格点上确定一个点P,使△B C1P是以B C1为底的等腰直角三角形,画出△B C1P,并写出所有P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个二次三项式,形式如下:
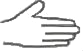 ﹣3x=x2﹣5x+1
﹣3x=x2﹣5x+1
(1)求所捂的二次三项式;
(2)若x=![]() +1,求所捂二次三项式的值;
+1,求所捂二次三项式的值;
(3)如果![]() +1的整数部分为a,则a2= .
+1的整数部分为a,则a2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
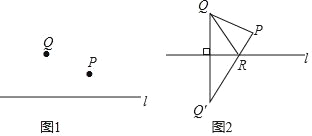
如图1,P,Q是直线l同侧两点,请你在直线l上确定一个点R,使△PQR的周长最小.
小阳的解决方法如下:
如图2,
(1)作点Q关于直线l的对称点Q;
(2)连接PQ′交直线l于点R;
(3)连接RQ,PQ.
所以点R就是使△PQR周长最小的点.
老师说:“小阳的作法正确.”
请回答:小阳的作图依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x= ![]() . ①求该抛物线的函数解析式;
. ①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com