
【题目】如图,在△ABC中,AB=4,D是AB上的一点(不与点A、B重合),DE∥BC,交AC于点E,则 ![]() 的最大值为 .
的最大值为 . 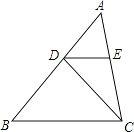
【答案】![]()
【解析】解:设AD=x, ![]() =y, ∵AB=4,AD=x,
=y, ∵AB=4,AD=x,
∴ ![]() =(
=( ![]() )2=(
)2=( ![]() )2 ,
)2 ,
∴ ![]() =
= ![]() x2①,
x2①,
∵DE∥BC,
∴△ADE∽△ABC,
∴ ![]() =
= ![]() ,
,
∵AB=4,AD=x,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵△ADE的边AE上的高和△CED的边CE上的高相等,
∴ ![]() =
= ![]() =
= ![]() ②,
②,
①÷②得:
∴y= ![]() =﹣
=﹣ ![]() x2+
x2+ ![]() x,
x,
∵AB=4,
∴x的取值范围是0<x<4;
∴y= ![]() =﹣
=﹣ ![]() (x﹣2)2+
(x﹣2)2+ ![]() ≤
≤ ![]() ,
,
∴ ![]() 的最大值为
的最大值为 ![]() .
.
所以答案是: ![]() .
.
【考点精析】通过灵活运用二次函数的最值和相似三角形的判定与性质,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】一个布袋中装有只有颜色不同的a(a>12)个球,分别是2个白球,4个黑球,6个红球和b个黄球,从中任意摸出一个球,把摸出白球,黑球,红球的概率绘制成统计图(未绘制完整).请补全该统计图并求出 ![]() 的值.
的值. 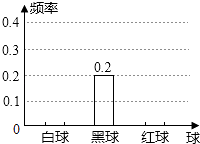
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明一家利用国庆八天驾车到某景点旅游,小汽车出发前油箱有油35L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图像回答下列问题:
(1)小汽车行驶______h后加油,中途加油_______L
(2)求加油前油箱余油量Q与行驶时间t的函数关系式
(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速80km/h,要到达目的地,油箱中的油是否够用?请说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线l:y=﹣x+2与y轴交于点A,抛物线y=(x﹣1)2+k经过点A,其顶点为B,另一抛物线y=(x﹣h)2+2﹣h(h>1)的顶点为D,两抛物线相交于点C.
(1)求点B的坐标,并说明点D在直线l上的理由;
(2)设交点C的横坐标为m.
交点C的纵坐标可以表示为:或;
(3)如图2,若∠ACD=90°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,BP、CP分别平分△ABC的外角∠CBD、∠BCE,BQ、CQ分别平分∠PBC、∠PCB,BM、CN分别是∠PBD、∠PCE的角平分线.
(1)当∠BAC=40°时,∠BPC= ,∠BQC= ;
(2)当BM∥CN时,求∠BAC的度数;
(3)如图②,当∠BAC=120°时,BM、CN所在直线交于点O,直接写出∠BOC的度数.
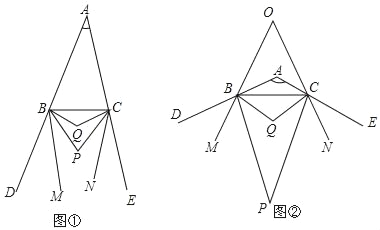
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+4与x轴、y轴分别交于点A、B,点C从点B出发,以每秒5个单位长度的速度向点A匀速运动;同时点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,到达终点后运动立即停止.连接CD,取CD的中点E,过点E作EF⊥CD,与折线DO﹣OA﹣AC交于点F,设运动时间为t秒.
x+4与x轴、y轴分别交于点A、B,点C从点B出发,以每秒5个单位长度的速度向点A匀速运动;同时点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,到达终点后运动立即停止.连接CD,取CD的中点E,过点E作EF⊥CD,与折线DO﹣OA﹣AC交于点F,设运动时间为t秒.
(1)点C的坐标为(用含t的代数式表示);
(2)求证:点E到x轴的距离为定值;
(3)连接DF、CF,当△CDF是以CD为斜边的等腰直角三角形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒 ![]() 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.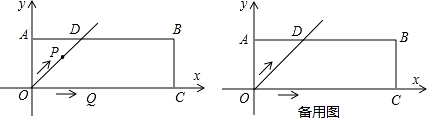
(1)当点P移动到点D时,求出此时t的值;
(2)当t为何值时,△PQB为直角三角形;
(3)已知过O、P、Q三点的抛物线解析式为y=﹣ ![]() (x﹣t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(x﹣t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com