
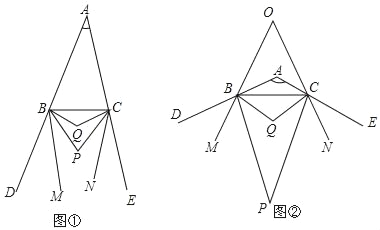
【题目】已知:如图①,BP、CP分别平分△ABC的外角∠CBD、∠BCE,BQ、CQ分别平分∠PBC、∠PCB,BM、CN分别是∠PBD、∠PCE的角平分线.
(1)当∠BAC=40°时,∠BPC= ,∠BQC= ;
(2)当BM∥CN时,求∠BAC的度数;
(3)如图②,当∠BAC=120°时,BM、CN所在直线交于点O,直接写出∠BOC的度数.
【答案】(1) 70°,125°;(2) ∠BAC=60° (3) 45°
【解析】
(1)根据三角形的外角性质分别表示出∠DBC与∠BCE,再根据角平分线的性质可求得∠CBP+∠BCP,最后根据三角形内角和定理即可求解;根据角平分线的定义得出∠QBC=![]() ∠PBC,∠QCB=
∠PBC,∠QCB=![]() ∠PCB,求出∠QBC+∠QCB的度数,根据三角形内角和定理求出即可;
∠PCB,求出∠QBC+∠QCB的度数,根据三角形内角和定理求出即可;
(2)根据平行线的性质得到∠MBC+∠NCB=180°,依此求解即可;
(3)根据题意得到∠MBC+∠NCB,再根据三角形外角的性质和三角形内角和定理得到∠BOC的度数.
(1)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=180°+∠A=220°,
∵BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,
∴∠CBP+∠BCP=![]() (∠DBC+∠BCE)=110°,
(∠DBC+∠BCE)=110°,
∴∠BPC=180°﹣110°=70°,
∵BQ、CQ分别是∠PBC、∠PCB的角平分线,
∴∠QBC=![]() ∠PBC,∠QCB=
∠PBC,∠QCB=![]() ∠PCB,
∠PCB,
∴∠QBC+∠QCB=55°,
∴∠BQC=180°﹣55°=125°;
(2)∵BM∥CN,
∴∠MBC+∠NCB=180°,
∵BM、CN分别是∠PBD、∠PCE的角平分线,
∴![]() (∠DBC+∠BCE)=180°,
(∠DBC+∠BCE)=180°,
即![]() (180°+∠BAC)=180°,
(180°+∠BAC)=180°,
解得∠BAC=60°;
(3)∵∠BAC=120°,
∴∠MBC+∠NCB=![]() (∠DBC+∠BCE)=
(∠DBC+∠BCE)=![]() (180°+α)=225°,
(180°+α)=225°,
∴∠BOC=225°﹣180°=45°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】设y=kx,是否存在实数k,使得代数式(x2﹣y2)(4x2﹣y2)+3x2(4x2﹣y2)能化简为x4?若能,请求出所有满足条件的k的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一直角坐标系中,直线y=﹣x+3与y=3x﹣5相交于C点,分别与x轴交于A、B两点.P、Q分别为直线y=﹣x+3与y=3x﹣5上的点.
(1)求△ABC的面积;
(2)若P、Q关于原点成中心对称,求P点的坐标;
(3)若△QPC≌△ABC,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G. 
求证:
(1)∠1=∠2;
(2)DG=B′G.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD⊥BC,AD=4,CE平分∠ACB交AD于点E.以线段CE为弦作⊙O,且圆心O落在AC上,⊙O交AC于点F,交BC于点G. 
(1)求证:AD与⊙O的相切;
(2)若点G为CD的中点,求⊙O的半径;
(3)判断点E能否为AD的中点,若能则求出BC的长,若不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题: 
(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1). ①画出△ABC关于y轴对称的△A1B1C1 , 并写出点C1的坐标;
②连结BC1 , 在坐标平面的格点上确定一个点P,使△B C1P是以B C1为底的等腰直角三角形,画出△B C1P,并写出所有P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com